Colles de mathématiques
Noyau d'un endomorphisme et de son carré
Sujet
Soit E un espace vectoriel et f∈ℒ(E).
- Montrer que ker(f ) = ker(f 2) ⇔ Im(f )∩ker(f ) = {0} .
- Montrer que ker(f ) = ker(f 2) ⇔ Im(f )⊕ker(f ) = E .
- Montrer que ker(f ) = ker(f 2) ⇔ Im(f ) = Im(f 2).
Corrigé de l'exercice de maths: Applications linéaires
Correction
- Supposons que
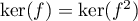 et soit
et soit  .
.
Il existe donc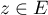 tel que
tel que 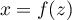 et aussi
et aussi  .
.
On a alors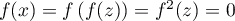 et donc
et donc 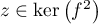 .
.
Or, , et donc
, et donc 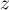 appartient aussi à
appartient aussi à 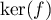 ,
c'est-à-dire
,
c'est-à-dire 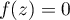 et donc, comme
et donc, comme 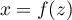 , on a
, on a  .
.
Ainsi, a obtenu que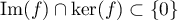 .
Comme on a toujours par ailleurs
.
Comme on a toujours par ailleurs  ,
on vient donc de montrer que
,
on vient donc de montrer que
![\[\ker(f)=\ker(f^2)\Longrightarrow\textrm{Im}(f)\cap\ker(f)=\la0\ra\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/16.png)
Réciproquement, supposons que .
.
Soit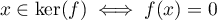 , donc
, donc  et donc
et donc
 (on peut d'ailleurs remarquer que cette inclusion est toujours vraie).
(on peut d'ailleurs remarquer que cette inclusion est toujours vraie).
Soit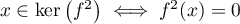 et soit
et soit 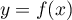 .
.
On a donc et donc
et donc 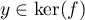 .
.
Or, par définition de on a justement
on a justement 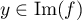 .
.
Comme on a supposé que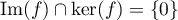 , on a donc nécessairement que
, on a donc nécessairement que  ,
donc
,
donc 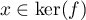 .
.
On vient donc de démontrer que , et donc, avec la paragraphe précédent, que
, et donc, avec la paragraphe précédent, que
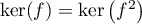 , et donc finalement que
, et donc finalement que
![\[\textrm{Im}(f)\cap\ker(f)=\la0\ra\Longrightarrow\ker(f)=\ker(f^2)\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/32.png)
On a donc démontrer la condition nécessaire et suffisante, donc l'équivalence.
- Si
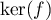 et
et  sont en somme directe alors, en particulier,
leur intersection est réduite à
sont en somme directe alors, en particulier,
leur intersection est réduite à 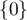 , et donc,
d'après la question précédente, on doit avoir
, et donc,
d'après la question précédente, on doit avoir  .
.
Réciproquement, supposons que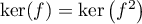 , et donc, d'après la question précédente,
que
, et donc, d'après la question précédente,
que 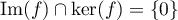 ,
,
L'image et le noyau de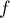 sont donc en somme directe, et
sont donc en somme directe, et
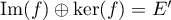 est un sous-espace de
est un sous-espace de 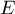 de dimension
de dimension
![\[\dim\left( E'\rp=\dim\left(\textrm{Im}(f)\rp+\dim\left(\ker(f)\rp\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/42.png)
Or, le théorème du range nous donne justement que
![\[\dim\lp\textrm{Im}(f)\rp+\dim\lp\ker(f)\rp=\dim(E)\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/43.png)
Ainsi, , c'est-à-dire
que
, c'est-à-dire
que 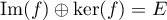 .
.
Finalement, on a montré la condition nécessaire et suffisante et donc l'équivalence
![\[\ker(f)=\ker(f^2)\iff \textrm{Im}(f)\oplus\ker(f)=E\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/46.png)
- Supposons que
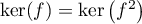 , alors le théorème du rang nous donne que
, alors le théorème du rang nous donne que
![\[\dim(E)=\dim\lp\textrm{Im}(f)\rp+\dim\lp\ker(f)\rp\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/48.png)
soit
![\[\dim\lp\textrm{Im}(f)\rp=\dim(E)-\dim\lp\ker(f)\rp
=\dim(E)-\dim\ker\left( f^2\right)
=\dim\lp\textrm{Im}\lp f^2\rp\rp\]](/Generateur-Devoirs/Colles/Applin/exAL10_c/49.png)
Comme de plus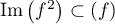 car
si
car
si 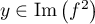 alors pour un certain
alors pour un certain 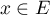 ,
,
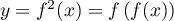 et donc
et donc 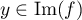 ,
on en déduit que
,
on en déduit que 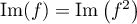 .
.
La réciproque peut se traiter identiquement, car de la même façon le théorème du rang nous fournit que si donc
donc
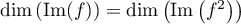 et
comme on a toujours l'inclusion
et
comme on a toujours l'inclusion 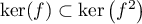 on a nécessairement
on a nécessairement
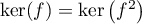 .
.