Colles de mathématiques
Produit, logarithme et intégrales et équivalent en l'infini
Exercice de maths: Intégrales sur un segment
Sujet
- Calculer l'intégrale
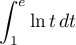
- Montrer que, pour tout
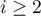 ,
,
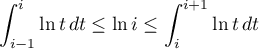 .
. - Montrer que, pour tout entier
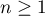 ,
,
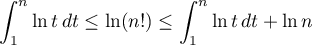 .
. - En déduire que
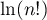 est équivalent à
est équivalent à 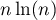 lorsque
lorsque 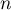 tend vers
tend vers 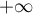 .
.