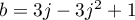🔍

Colles de mathématiques

Quelques calculs algébriques avec j


Sujet


On note 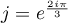$j=e^{\frac{2i\pi}{3}}$.
  1. Calculer $1+j+j^2$.
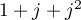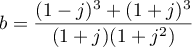  2. Écrire sous forme algébrique le nombre $b=\dfrac{(1-j)^3+(1+j)^3}{(1+j)(1+j^2)}$.

Corrigé de l'exercice de maths: Nombres complexes

Correction


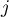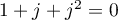
  1. $j$ est une racine 3ème de l'unité, donc $1+j+j^2=0$
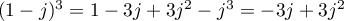
  2. On a donc $(1-j)^3=1-3j+3j^2-j^3=-3j+3j^2$
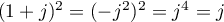
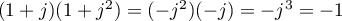
    $(1+j)^2=(-j^2)^2=j^4=j$ $(1+j)(1+j^2)=(-j^2)(-j)=-j^3=-1$
    et enfin, $b=3j-3j^2+1$