Colles de mathématiques
Rayon de convergence
Sujet
Déterminer le rayon de convergence de la série entière
∑
n≥1
an zn,
pour
a≥0.
Corrigé de l'exercice de maths: Séries entières
Correction
Pour  le terme général est nul et la série converge trivialement pour tout
le terme général est nul et la série converge trivialement pour tout 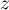 .
.
Pour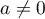 , on applique la règle de d'Alembert à
, on applique la règle de d'Alembert à 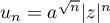 :
:
![\[\frac{u_{n+1}}{u_n}=|z|a^{\sqrt{n+1}-\sqrt{n}}\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC11_c/5.png)
Or,
![\[\begin{array}{ll}\sqrt{n+1}-\sqrt{n}&=\sqrt{n}\big((1+1/n)^{1/2}-1)\\[.7em]
&=\sqrt{n}\left(1+\frac{1}{2n}-1+o\left(\frac1n\right)\right)\to 0\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC11_c/6.png)
Ainsi, on obtient que
![\[\frac{u_{n+1}}{u_n}\to |z|a^0=|z|\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC11_c/7.png)
et on en déduit que la série converge absolument pour et diverge pour
et diverge pour 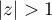 .
.
Le rayon de convergence de la série entière est donc 1.
Pour
Or,
![\[\begin{array}{ll}\sqrt{n+1}-\sqrt{n}&=\sqrt{n}\big((1+1/n)^{1/2}-1)\\[.7em]
&=\sqrt{n}\left(1+\frac{1}{2n}-1+o\left(\frac1n\right)\right)\to 0\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC11_c/6.png)
Ainsi, on obtient que
et on en déduit que la série converge absolument pour
Le rayon de convergence de la série entière est donc 1.