🔍

Colles de mathématiques

Rayon de convergence


Sujet


Déterminer le rayon de convergence de la série entière   ∑ n nln(n) zn

Corrigé de l'exercice de maths: Séries entières

Correction


Soit 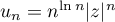$u_n=n^{\ln n}|z|^n$ le terme général, ou aussi
\[\begin{array}{ll}u_n&=|z|e^{\ln\left( n\ln n\right)}=|z|e^{\ln n \times \ln n}\\[.5em]&=|z|e^{\left(\ln n\right)^2}\enar\]

et alors
\[\dfrac{u_{n+1}}{u_n}=\left|z\right|e^{\lp\ln(n+1)\rp^2-\lp\ln n\rp^2}\]

avec
\[\begin{array}{ll}\lp\ln(n+1)\rp^2-\lp\ln n\rp^2 &=\Bigl(\ln(n+1)-\ln(n)\Bigr)\,\Bigl(\ln(n+1)+\ln(n)\Bigr)\\[.7em] &=\ln\lp\dfrac{n+1}{n}\rp\,\ln\lp n(n+1)\rp \\[.8em] &=\ln\lp1+\dfrac1n\rp\ln\lp n(n+1)\rp \\[.8em] &\underset{+\infty}{\sim}\dfrac1n\ln\left( n^2\right) =\dfrac{2\ln n}{n} \underset{+\infty}{\longrightarrow}0 \enar\]

et ainsi,
\[\dfrac{u_{n+1}}{u_n}=\left|z\right|e^{\lp\ln(n+1)\rp^2-\lp\ln n\rp^2}\underset{+\infty}{\longrightarrow}\left|z\right|\]

et le rayon de convergence est 1.


On peut aussi utiliser la règle de Cauchy :
\[\sqrt[n]{u_n}=n^{\ln n/n}|z|=\exp\big((\ln n\times\ln n)/n\big)|z|\to |z|\]

La série est donc convergente pour $|z|<1$ et divergente pour $|z|>1$.
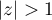Son rayon de convergence vaut 1.