🔍

Colles de mathématiques

Rayon de convergence


Sujet


Déterminer le rayon de convergence de la série entière   ∑ n nx2n/2n + 1

Corrigé de l'exercice de maths: Séries entières

Correction


Pour 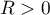$R>0$, on a
\[\frac{\sqrt nR^{2n}}{2^n+1}\underset{+\infty}{\sim} \sqrt n \left(\frac{R^2}{2}\right)^n\]

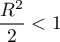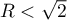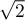Ce terme général est borné si et seulement si $\dfrac{R^2}{2}<1$, soit $R<\sqrt2$. Le rayon de convergence est donc $\sqrt2$.

On peut aussi utiliser la règle de d'Alembert en posant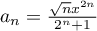 $a_n=\frac{\sqrt nx^{2n}}{2^n+1}$, et alors
\[\dfrac{a_{n+1}}{a_n}=x^2\sqrt{1+\dfrac1n}\dfrac{2^n+1}{2^{n+1}+1}\underset{+\infty}{\sim}\dfrac{x^2}{2}\]

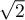et on retrouve le rayon de convergence de $\sqrt2$.