Colles de mathématiques
Rayon de convergence
Sujet
Déterminer le rayon de convergence de la série entière
∑
n
(2 + ni ) zn
Corrigé de l'exercice de maths: Séries entières
Correction
On remarque que, d'après les inégalités triangulaires,
![\[(n-2)|z|^n\leq |2+ni||z^n|\leq (2+n)|z|^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exRC6_c/1.png)
Ainsi, la série converge pour
et diverge pour 
.
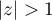Son rayon de convergence est donc 1.
On (re)trouve aussi ce résultat avec la règle de d'Alembert.
Ainsi, la série converge pour
et diverge pour .
Son rayon de convergence est donc 1.
On (re)trouve aussi ce résultat avec la règle de d'Alembert.