Colles de mathématiques
Recherche de fonctions avec une propriété intégrale
Retour
Sujet
Déterminer les fonctions f: [0; 1][0; 1] continues
et telles que
∫
0
1
f (x) dx
=
∫
0
1
f 2(x) dx .
Corrigé de l'exercice de maths: Intégrales sur un segment
Correction
Par linéarité,
![\[\int_0^1f(x)dx=\int_0^1f^2(x)dx
\iff \int_0^1\Bigl(f(x)-f^2(x)\Bigr)dx=
\int_0^1 f(x)\Bigl(1-f(x)\Bigr)dx=0\]](/Generateur-Devoirs/Colles/Integrale/exR2_c/1.png)
Or, sur![$[0;1]$](/Generateur-Devoirs/Colles/Integrale/exR2_c/2.png) ,
, ![$f(x)\in[0;1]$](/Generateur-Devoirs/Colles/Integrale/exR2_c/3.png) et donc, en particulier,
et donc, en particulier,
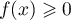 et
et 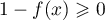 ,
d'où on doit avoir nécessairement,
pour tout
,
d'où on doit avoir nécessairement,
pour tout ![$x\in[0;1]$](/Generateur-Devoirs/Colles/Integrale/exR2_c/6.png) ,
,
 ,
soit
,
soit 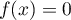 ou
ou  .
.
Comme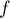 est continue, on a alors nécessairement
est continue, on a alors nécessairement 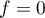 sur
sur ![$[0,1]$](/Generateur-Devoirs/Colles/Integrale/exR2_c/12.png) ou
ou
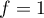 sur
sur ![$[0;1]$](/Generateur-Devoirs/Colles/Integrale/exR2_c/14.png) .
.
Réciproquement, ces deux fonctions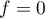 et
et 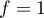 conviennent bien.
conviennent bien.
Remarque: bien sûr, si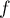 n'est pas supposée continue,
la fonction définie par
n'est pas supposée continue,
la fonction définie par
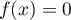 si
si 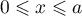 et
et  si
si 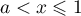 convient aussi pour tout
convient aussi pour tout ![$a\in]0;1[$](/Generateur-Devoirs/Colles/Integrale/exR2_c/22.png) .
.
Or, sur
Comme
Réciproquement, ces deux fonctions
Remarque: bien sûr, si