Colles de mathématiques

Énoncer et démontrer le théorème de Rolle.

Théorème: Soit f une fonction continue sur [a; b] et dérivable sur ]a; b[ et telle que f (a) = f (b), alors il existe c∈]a; b[ tel que f '(c) = 0



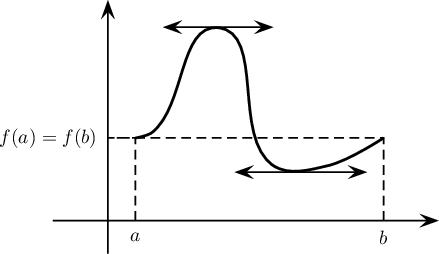
Démonstration:
La démonstration peut être vue comme une conséquence de la propriété des fonctions continues: si f est continue sur [a; b], alors f est bornée et atteint ses bornes.
f atteint par exemple en c un maximum ou un minimum et donc f atteint par exemple en c est un point critique c'est-à-dire f '(c) = 0.
Le seul point qui reste à vérifie est que c∈]a; b[, c'est-à-dire que c≠a et c≠b. Ceci est en effet le cas lorsque f n'est pas constante.

Plus précisément, si f est constante sur [a; b], alors pour tout x∈[a; b], on a f '(x) = 0, et le théorème est clairement vérifié.

Sinon, comme f est continue sur [a; b], f y est bornée, et on pose m = inf{f(x) ; x∈[a, b]} et M = sup{f(x) ; x∈[a, b]}.
Comme f n'est pas constante, on a m < M, et soit donc m < f(a) = f(b) soit f(a) = f(b) < M.
Dans le premier cas par exemple, il existe donc c∈]a; b[ tel que f(c) = m et en ce point critique f '(c) = 0.
Le raisonnement est analogue dans le deuxième cas.