Colles de mathématiques
Application linéaire ? Noyau et image ?
Sujet
L'application f : R2R3 définie par f (x, y) = (x + y, x − 2y, 1) est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Corrigé de l'exercice de maths: Applications linéaires
Correction
f ne peut pas être linéaire car 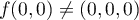 (si elle l'était on devrait en effet avoir
(si elle l'était on devrait en effet avoir
 pour tous
pour tous 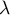 et
et 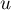 , en particulier donc pour
, en particulier donc pour 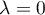 …).
…).
Ceci ne l'empêche pas de pouvoir être éventuellement injective, surjective, bijective.
Le noyau de est vide: pour tout
est vide: pour tout 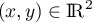 ,
, 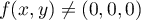 et donc
et donc 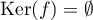 .
.
Attention, même si on avait trouvé un noyau réduit au vecteur nul, cela n'aurait pas permis de conclure à l'injectivité de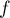 car elle n'est pas linéaire. Il faut revenir à la définition.
Soit deux couples de
car elle n'est pas linéaire. Il faut revenir à la définition.
Soit deux couples de 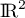 ,
, 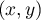 et
et 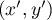 tels que
tels que
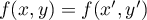 alors
alors
![\[\la\begin{array}{ll}
x+y=x'+y' \\
x-2y=x'-2y'\\
1=1\enar\right.\]](/Generateur-Devoirs/Colles/Applin/exAL2_c/16.png)
soit, en soustrayant les deux premières équations,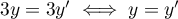 et donc la première équation donne
et donc la première équation donne
 .
.
L'application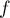 est donc injective.
est donc injective.
Étudions maintenant l'image: soit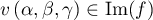 ,
alors il existe
,
alors il existe 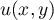 tel que
tel que  ,
,
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=1\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=1\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL2_c/23.png)
Ainsi, tout et donc
et donc
 (qui n'est pas un espace vectoriel).
(qui n'est pas un espace vectoriel).
f n'est donc pas surjective, et pas non plus bijective.
Ceci ne l'empêche pas de pouvoir être éventuellement injective, surjective, bijective.
Le noyau de
Attention, même si on avait trouvé un noyau réduit au vecteur nul, cela n'aurait pas permis de conclure à l'injectivité de
![\[\la\begin{array}{ll}
x+y=x'+y' \\
x-2y=x'-2y'\\
1=1\enar\right.\]](/Generateur-Devoirs/Colles/Applin/exAL2_c/16.png)
soit, en soustrayant les deux premières équations,
L'application
Étudions maintenant l'image: soit
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=1\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=1\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL2_c/23.png)
Ainsi, tout
f n'est donc pas surjective, et pas non plus bijective.