Colles de mathématiques
Calcul matriciel - Inverse d'une matrice 4x4
Exercice de maths: Matrices
Sujet
On considère la matrice carrée
 .
.
 .
.
- Calculer
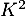 .
.
- En déduit que
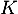 est inversible et calculer
est inversible et calculer 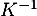 .
.
- Soit
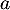 et
et 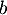 deux réels. On définit la matrice
deux réels. On définit la matrice
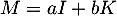 .
Montrer que
.
Montrer que 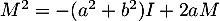 .
.
- En déduire que si
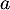 et
et 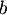 ne sont pas tous les deux nuls,
ne sont pas tous les deux nuls, 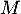 est inversible.
est inversible.
- En déduire l'inverse de la matrice
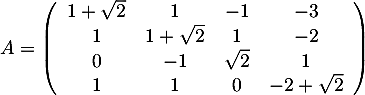 .
.