Colles de mathématiques
Matrice nilpotente et calcul d'inverse
Exercice de maths: Matrices
Sujet
Soit 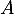 une matrice nilpotente, c'est-à-dire telle qu'il existe un entier
une matrice nilpotente, c'est-à-dire telle qu'il existe un entier 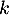 tel que
tel que 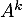 est la matrice nulle.
est la matrice nulle.
Montrer que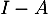 est inversible et que son inverse s'écrit sous la forme
est inversible et que son inverse s'écrit sous la forme 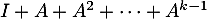 .
.
En déduire l'inverse de la matrice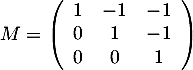 .
.
Montrer que
En déduire l'inverse de la matrice
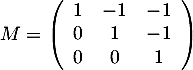 .
.