Colles de mathématiques
Coefficients binomiaux, puissance n-ième et inverse
Exercice de maths: Matrices
Sujet
Soit  un entier naturel.
un entier naturel.
- Soit
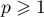 un entier.
Montrer que
un entier.
Montrer que 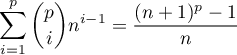 .
.
- Soit
 la matrice de
la matrice de 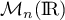 dont tous les coefficients valent 1.
Calculer
dont tous les coefficients valent 1.
Calculer  pour tout
pour tout 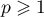 .
.
- Soit
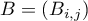 la matrice carrée de taille
la matrice carrée de taille 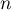 définie par
définie par
![\[b_{i,j}=\la\begin{array}{rcl}2&\text{ si } &i=j\\1&\text{ si } &i\not=j\enar\right.\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse/10.png)
Calculer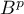 pour
pour  .
.
- Montrer que
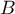 est inversible et calculer son inverse.
est inversible et calculer son inverse.