Colles de mathématiques
Caractérisation d'un endomorphisme diagonalisable
Oral ENS Ulm, filière B/L, 2017
Exercice de maths: Diagonalisation - Annales ENS Ulm - B/L
Sujet
Pour des endomorphismes 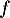 et
et 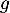 de
de 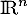 , on note
, on note 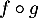 la composée de
la composée de 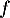 et
et 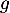 et
et 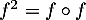 .
On note
.
On note  l’endomorphisme identité de
l’endomorphisme identité de 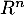 .
Pour un endomorphisme
.
Pour un endomorphisme 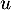 de
de 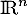 , soit
, soit 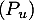 la propriété:
la propriété:
![\[\forall \lambda\in\R, Ker(u-\lambda Id) = Ker (u-\lambda Id)^2\]](/Generateur-Devoirs/Colles/Diagonalisation/crctdiago/13.png)
Première partie. Soit et
et 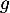 deux endomorphismes de
deux endomorphismes de  tels que
tels que  .
.
Première partie. Soit
- Montrer que
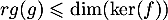 .
.
- Montrer que
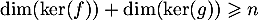 .
.
- Soit
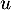 un endomorphisme de
un endomorphisme de 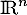 tel que
tel que
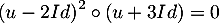 .
.
Montrer que et
et 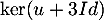 sont supplémentaires dans
sont supplémentaires dans 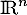 .
.
- Si
 vérifie de plus
vérifie de plus 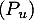 , montrer que
, montrer que 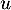 est diagonalisable.
est diagonalisable.
Deuxième partie. Soit un endomorphisme de
un endomorphisme de 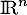 .
.
- Soit
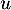 un endomorphisme diagonalisable. Montrer que
un endomorphisme diagonalisable. Montrer que  vérifie
vérifie 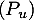 .
.
- Réciproquement, si
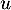 vérifie
vérifie 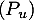 , est-ce que u est diagonalisable ?
, est-ce que u est diagonalisable ?