🔍

Colles de mathématiques

Convergence de la "demi somme harmonique" - Inégalité des accroissements finis


Sujet


  1. Démontrer que pour tout x≥0, on a 1x + 1 ≤ ln(x + 1) − ln(x) ≤ 1x
  2. On pose vn = 1n + 1 + … + 12n .
    Démontrer que
    ln(2n+1) − ln(2n) ≤ vn ≤ ln(2n) − ln(n)
    En déduire que (vn).

Corrigé de l'exercice de maths: Suites

Correction


  1. Applique le théorème des accroissements finis à la fonction 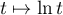$t\mapsto \ln t$ sur l'intervalle $[x,x+1]$: il existe $\theta\in ]x,x+1[$ tel que
    \[\ln(x+1)-\ln x=\frac{x+1-x}\theta=\frac 1\theta\]

    On conclut car
    \[0\leqslant x\leqslant\theta\leqslant x+1 \implies \frac1{x+1}\leqslant\frac 1\theta\leqslant\frac 1x\]

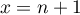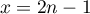  2. On applique l'inégalité précédente pour $x=n$, $x=n+1$, $x=n+2$ jusque $x=2n-1$. On somme ces inégalités et on obtient, en ne gardant que l'inégalité de gauche:
    \[v_n\leqslant\ln(2n)-\ln n\]

    On applique ensuite l'inégalité précédente pour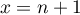 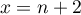$x=n+1$, $x=n+2$ jusque $x=2n$ et on ne garde cette fois que l'inégalité de droite et on obtient
    \[\ln(2n+1)-\ln (n+1)\leqslant v_n\]

    Ceci se réécrit encore en
    \[\ln\lp\frac{2n+1}{n+1}\rp\leqslant v_n\leqslant\ln\lp\frac{2n}n\rp=\ln 2\]

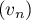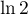    Par le théorème des gendarmes, on en déduit que $(v_n)$ converge vers $\ln 2$.