Colles de mathématiques
Décomposition en éléments simples
Sujet
Décomposer en éléments simples
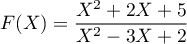
Corrigé de l'exercice de maths: Polynômes
Correction
On a 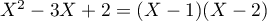 et donc,
comme
et donc,
comme 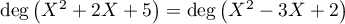 il y a une partie entière de degré nul, donc une constante,
et alors
il y a une partie entière de degré nul, donc une constante,
et alors
![\[F(X)=\dfrac{X^2+2X+5}{X^2-3X+2}
=\dfrac{X^2+2X+5}{(X-1)(X-3)}
=a+\dfrac{b}{X-1}+\dfrac{c}{X-2}\]](/Generateur-Devoirs/Colles/Polynomes/exEltSimples1_c/3.png)
En faisant tendre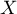 vers
vers 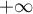 , on trouve
, on trouve  .
.
En multipliant par puis en faisant
puis en faisant  ,
on obtient
,
on obtient 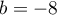 ,
puis, de même,
En multipliant par
,
puis, de même,
En multipliant par  puis en faisant
puis en faisant  ,
on obtient
,
on obtient  .
.
En résumé, on a
![\[F(X)=\dfrac{X^2+2X+5}{X^2-3X+2}
=1-\dfrac{8}{X-1}+\dfrac{13}{X-2}\]](/Generateur-Devoirs/Colles/Polynomes/exEltSimples1_c/13.png)
En faisant tendre
En multipliant par
En résumé, on a