🔍

Colles de mathématiques

Équation polynomiale

Oral ENSAE, Saclay, filière B/L, 2014/2015



Exercice de maths: Polynômes - Annales ENSAE - Saclay - B/L

Sujet


Soit 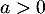$a>0$. On cherche le degré des polynômes vérifiant:
\[\forall x\in[0;2a], \ \dfrac12f(x)=f\lp\dfrac{x}2\rp+f\lp a-\dfrac{x}2\rp\]

On note $M=\underset{t\in[0;2a]}{\max}f''(t)$.
  1. Montrer qu'il existe $c\in[0;2a]$ tel que $f''(c)=M$.
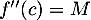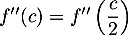  2. Montrer que $f''(c)=f''\lp\dfrac{c}2\rp$.
  3. Montrer que l'on aurait pu choisir $c$ dans $[0;a]$.
  4. Montrer que 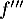$f'''$ s'annule une infinité de fois. Conclure.

Correction