Colles de mathématiques
Décomposition en série de Fourier
Sujet
Étudier la série de Fourier de la fonction
f, 2π-périodique, définie par sa représentation graphique suivante:
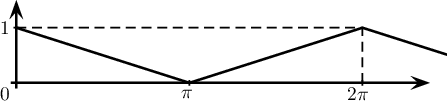

Corrigé de l'exercice de maths: Série de Fourier
Correction
f est 2π-périodique et paire, donc bn,
et
![\[\begin{array}{ll}
a_0&\dsp=\dfrac{2}{2\pi}\int_0^\pi f(x)dx
=\dfrac1\pi\int_0^\pi \lp-\dfrac1\pi x+1\right) dx\\[1em]
&=\dfrac1\pi\Bigl[-\dfrac{1}{2\pi}x^2+x\Bigr]_0^\pi
=\dfrac1\pi\left( -\dfrac12\pi+pi\right)
=\dfrac12\enar\]](/Generateur-Devoirs/Colles/fourier/ex1_c/4.png)
et pour tout entier n>0,
![\[a_n=\dfrac{4}{\pi}\int_0^\pi f(x)\cos(n\omega x)dx\]](/Generateur-Devoirs/Colles/fourier/ex1_c/6.png)
avec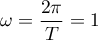 ,
et sur
,
et sur ![$[0;2\pi]$](/Generateur-Devoirs/Colles/fourier/ex1_c/8.png) ,
, 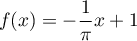 ,
et donc
,
et donc
![\[\begin{array}{ll}
a_n&\dsp=\dfrac{4}{\pi}\int_0^\pi \lp-\dfrac1\pi x+1\right) \cos(nx)dx
=\dfrac{4}{n\pi}\Bigl[\lp-\dfrac1\pi x+1\rp\sin(nx)\Bigr]_0^\pi
+\dfrac{4}{n\pi^2}\int_0^\pi \sin(nx)dx \\[1em]
&=0-\dfrac{4}{n^2\pi^3}\Bigl[\cos(nx)\Bigr]_0^\pi
=-\dfrac{4}{n^2\pi^3}\Bigl(\cos(n\pi)-1\Bigr)\\[1em]
&=\dfrac{4}{n^2\pi^3}\Bigl(1-(-1)^n\Bigr)
\end{array}
\]](/Generateur-Devoirs/Colles/fourier/ex1_c/10.png)
ainsi,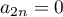 et
et 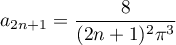 .
.
Comme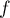 est continue sur
est continue sur 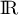 , on peut donc écrire que,
pour tout réel
, on peut donc écrire que,
pour tout réel 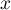 ,
,
![\[f(x)=\dfrac12
+\dfrac{8}{\pi^3}\sum_{n\geqslant0}\dfrac{\cos\left( (2n+1)x\right)}{(2n+1)^2}\]](/Generateur-Devoirs/Colles/fourier/ex1_c/16.png)
![\[\begin{array}{ll}
a_0&\dsp=\dfrac{2}{2\pi}\int_0^\pi f(x)dx
=\dfrac1\pi\int_0^\pi \lp-\dfrac1\pi x+1\right) dx\\[1em]
&=\dfrac1\pi\Bigl[-\dfrac{1}{2\pi}x^2+x\Bigr]_0^\pi
=\dfrac1\pi\left( -\dfrac12\pi+pi\right)
=\dfrac12\enar\]](/Generateur-Devoirs/Colles/fourier/ex1_c/4.png)
et pour tout entier n>0,
avec
![\[\begin{array}{ll}
a_n&\dsp=\dfrac{4}{\pi}\int_0^\pi \lp-\dfrac1\pi x+1\right) \cos(nx)dx
=\dfrac{4}{n\pi}\Bigl[\lp-\dfrac1\pi x+1\rp\sin(nx)\Bigr]_0^\pi
+\dfrac{4}{n\pi^2}\int_0^\pi \sin(nx)dx \\[1em]
&=0-\dfrac{4}{n^2\pi^3}\Bigl[\cos(nx)\Bigr]_0^\pi
=-\dfrac{4}{n^2\pi^3}\Bigl(\cos(n\pi)-1\Bigr)\\[1em]
&=\dfrac{4}{n^2\pi^3}\Bigl(1-(-1)^n\Bigr)
\end{array}
\]](/Generateur-Devoirs/Colles/fourier/ex1_c/10.png)
ainsi,
Comme
![\[f(x)=\dfrac12
+\dfrac{8}{\pi^3}\sum_{n\geqslant0}\dfrac{\cos\left( (2n+1)x\right)}{(2n+1)^2}\]](/Generateur-Devoirs/Colles/fourier/ex1_c/16.png)