Colles de mathématiques
Déterminer les polynômes tels que … (ter)
Retour
Sujet
Déterminer les polynômes de ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP22/1.png) tels que
tels que  .
.
Corrigé de l'exercice de maths: Polynômes
Correction
Le polynôme nul est solution.
Maintenant, si 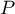 est un polynôme non nul solution, alors le degré de
est un polynôme non nul solution, alors le degré de
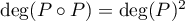 , et donc on doit avoir
, et donc on doit avoir
![\[\deg(P)^2=\deg(P)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP22_c/3.png)
On en déduit que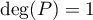 ou
ou 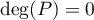 , c'est-à-dire que le polynôme
, c'est-à-dire que le polynôme 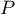 est de degré 1 ou 0.
est de degré 1 ou 0.
Soit donc , alors
, alors
![\[\begin{array}{lcl}
P\circ P(X)&=&a(aX+b)+b\\
&=&a^2X+(ab+b)\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP22_c/8.png)
et on doit donc avoir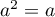 , soit
, soit  ou
ou  , et
, et 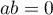 .
.
Si , alors nécessairement
, alors nécessairement 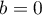 , tandis que si
, tandis que si  ,
alors
,
alors  peut être quelconque.
peut être quelconque.
Finalement, on trouve que les solutions sont les polynômes constants et le polynôme identité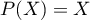 .
.
On en déduit que
Soit donc
et on doit donc avoir
Si
Finalement, on trouve que les solutions sont les polynômes constants et le polynôme identité