Colles de mathématiques
Déterminer les polynômes tels que … (ter) et le décomposer en produits de polynômes irréductibles
Sujet
Déterminer un polynôme  de degré 4 qui admet 2 comme racine double
et tel que
de degré 4 qui admet 2 comme racine double
et tel que 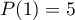 ,
,  et
et 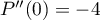 .
.
Décomposer alors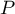 en produit de polynômes irréductibles
de
en produit de polynômes irréductibles
de ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3/6.png) puis de
puis de ![$\C[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3/7.png) .
.
Décomposer alors
Corrigé de l'exercice de maths: Polynômes - Nombres complexes
Correction
2 est une racine double de 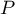 ,
donc
,
donc 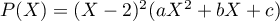 .
.
De plus,
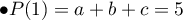
![$\begin{array}{ll}\bullet &P(X)=(X^2-4X+4)(aX^2+bX+c)\\[.4em]
&=aX^4+(-4a+b)X^3+(4a-4b+c)X^2+(4b-4c)X+4c\enar$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/4.png)
et donc .
.

En résumé, on obtient le système linéaire
![\[\la\begin{array}{rcrcrcrcr}
a&+&b&+&c&=&5 \\
&&b&-&c&=&0 \\
4a&-&4b&+&c&=&-2
\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/7.png)
qui est équivalent à et
et 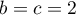 .
.
On trouve donc l'unique polynôme
On a, en calculant son discriminant ou en à l'aide de sa forme canonique: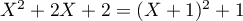 ce qui montre que
ce qui montre que 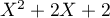 est irréductible dans
est irréductible dans
![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/13.png) , tandis que dans
, tandis que dans ![$\C[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/14.png) ,
,
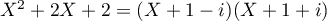 et donc
et donc
![\[\begin{array}{ll}P(X)&=(X-2)^2(X^2+2X+2)\\[.4em]
&=(X-2)^2(X+1-i)(X+1+i)\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/16.png)
De plus,
![$\begin{array}{ll}\bullet &P(X)=(X^2-4X+4)(aX^2+bX+c)\\[.4em]
&=aX^4+(-4a+b)X^3+(4a-4b+c)X^2+(4b-4c)X+4c\enar$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/4.png)
et donc
En résumé, on obtient le système linéaire
![\[\la\begin{array}{rcrcrcrcr}
a&+&b&+&c&=&5 \\
&&b&-&c&=&0 \\
4a&-&4b&+&c&=&-2
\enar\right.\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/7.png)
qui est équivalent à
On trouve donc l'unique polynôme
On a, en calculant son discriminant ou en à l'aide de sa forme canonique:
![\[\begin{array}{ll}P(X)&=(X-2)^2(X^2+2X+2)\\[.4em]
&=(X-2)^2(X+1-i)(X+1+i)\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP3_c/16.png)