🔍

Colles de mathématiques

Diagonalisabilité à partir d'une relation sur l'endomorphisme


Sujet


Soit u∈ℒ(E) tel que u2 = 3u − 2id.
  1. Montrer que Sp(u)⊂{1; 2}.
  2. Montrer que E1⊕E2 = E.
    Indication: on pourra utiliser la décomposition id = (u − id) − (u − 2id).
    Que peut-on en conclure ?

Corrigé de l'exercice de maths: Diagonalisation

Correction


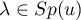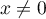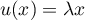  1. Soit $\lambda\in Sp(u)$, et $x\not=0$ tel que $u(x)=\lambda x$.
    On a alors, d'une part
    \[u^2(x)=u\lp\lambda x\rp=\lambda u(x)=\lambda^2x\]

    et d'autre part
    \[u^2(x)=(3u-2id)(x)=3\lambda x-2x\]

    On doit donc n'écessairement avoir
    \[\lambda^2x=3\lambda x-2x\iff \lp\lambda^2-3\lambda +2\right) x=0\]

    soit, puisque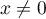 $x\not=0$,
    \[\lambda^2-3\lambda+2=0\]

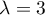    et donc, en résolvant cette équation du second degré, on trouve que $\lambda=1$ ou $\lambda=3$.
    On a donc bien trouvé la condition nécessaire
    \[\lambda\in Sp(u)\longrightarrow \lambda\in\la 1;2\ra\]

    c'est-à-dire l'inclusion
    \[Sp(u)\subset\la1;3\ra\]


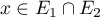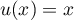  2. On a directement que si $x\in E_1\cap E_2$, alors $u(x)=x$ et à la fois 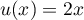$u(x)=2x$ et donc, $x=2x\iff x=0$.
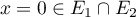    Réciproquement, si $x=0$, on a évidemment $u(0)=0=2\tm0$ et donc $x=0\in E_1\cap E_2$.
    Ainsi, on a montré que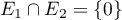 $E_1\cap E_2=\la0\ra$.

    Il reste à montrer la somme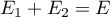 $E_1+E_2=E$.
    Soit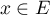 $x\in E$ alors, en utilisant l'indication, on écrit
    \[id(x)=x=\underbrace{(u-id)(x)}_{y_1}\quad\underbrace{-\ (u-2id)(x)}_{y_2}\]

    avec, en utilisant la relation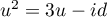 $u^2=3u-id$,
    \[\begin{array}{ll} u(y_1)&=u\lp(u-id)(x)\rp\\[.4em] &=u^2(x)-u(x)\\[.4em] &=3u(x)-2id(x)-u(x)\\[.4em] &=2u(x)-2id(x)\\[.4em] &=2(u-id)(x)=2y_1\enar\]

    ce qui montre que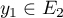 $y_1\in E_2$.

    On a de même $y_2\in E_1$ car
    \[\begin{array}{ll} u(y_1)&=u\lp-(u-2id)(x)\rp\\[.4em] &=-u^2(x)+2u(x)\\[.4em] &=-3u(x)+2id(x)+2u(x)\\[.4em] &=-u(x)+2id(x)\\[.4em] &=-(u-2id)(x)=y_2\enar\]

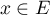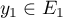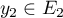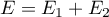    On a donc montré que pour tout $x\in E$, on a $x=y_1+y_2$ avec $y_1\in E_1$ et $y_2\in E_2$, c'est-à-dire que $E=E_1+E_2$.

    Finalement, on a bien montré que $E=E_1\oplus E_2$.

    On déduit enfin de ce qui précède que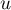 $u$ est diagonalisable.