Colles de mathématiques
DL, tangente et position relative
Sujet
Donner le développement limité en 0 puis en 1, à l'ordre 2,
de la fonction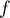 
définie par l'expression 
.
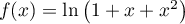Étudier la position relative de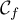
et de ses tangentes en 0 et 1.
définie par l'expression .
Étudier la position relative de
et de ses tangentes en 0 et 1.
Corrigé de l'exercice de maths: Développements limités
Correction
En 0, en posant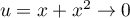 
, on a directement
![\[\begin{array}{ll}
\ln\lp1+x+x^2\rp&=\ln(1+u)=u-\dfrac12u^2\\
&=x+x^2-\dfrac12\left( x+x^2\rp^2+o\left( x^2\rp\\
&=x+\dfrac12x^2+o\left( x^2\rp\enar\]](/Generateur-Devoirs/Colles/DL/DL-tangente-position-relative_c/2.png)
La tangente en 0 a donc pour équation
,
et comme 
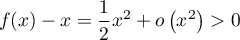, on en déduit
de plus que la courbe est est au dessus de cette tangente au voisinage de 0.
On procède de même en
, mais en posant tout d'abord 
où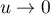 
, et alors
![\[\begin{array}{ll}
f(x)&=\ln\lp1+x+x^2\rp\\
&=\ln\Bigl(1+u+1+(u+1)^2\Bigr)\\
&=\ln\lp3+3u+u^2\rp\\
&=\ln3\lp1+u+\dfrac13u^2\rp\\
&=\ln3+\ln\lp1+u+\dfrac13u^2\rp\\
&=\ln3+\left( u+\dfrac13u^2\rp-\dfrac12\left( u+\dfrac13u^2\rp^2+o\left( u^2\rp\\
&=\ln3+u-\dfrac16u^2+o\left( u^2\rp\\
&=\ln3+(x-1)-\dfrac16(x-1)^2+o\left( (x-1)^2\rp\\
\enar\]](/Generateur-Devoirs/Colles/DL/DL-tangente-position-relative_c/8.png)
La tangente en 1 a donc pour équation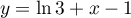
,
et comme
![\[f(x)-\lp\ln3+x-1\rp=-\dfrac16(x-1)^2+o\lp (x-1)^2\rp<0\]](/Generateur-Devoirs/Colles/DL/DL-tangente-position-relative_c/10.png)
on en déduit de plus que la courbe est est au dessous de cette tangente au voisinage de 1.
, on a directement
La tangente en 0 a donc pour équation
,
et comme , on en déduit
de plus que la courbe est est au dessus de cette tangente au voisinage de 0.
On procède de même en
, mais en posant tout d'abord où , et alors
La tangente en 1 a donc pour équation
,
et comme
on en déduit de plus que la courbe est est au dessous de cette tangente au voisinage de 1.