Colles de mathématiques
Égalité d'un polynôme et de l'exponentielle: finitude des solutions
Sujet
Soit P un polynôme.
Montrer que l'équation P(x) = ex n'admet qu'un nombre fini de solutions.
Montrer que l'équation P(x) = ex n'admet qu'un nombre fini de solutions.
Corrigé de l'exercice de maths: Théorèmes de Rolle & accroissements finis
Correction
Soit 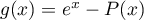 .
Si
.
Si 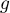 admet
admet 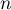 racines,
alors
racines,
alors 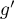 en admet
en admet  , d'après le théorème de Rolle.
En réappliquant ce théorème à
, d'après le théorème de Rolle.
En réappliquant ce théorème à  , on obtient que
, on obtient que 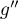 admet
admet
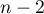 racines, et en réitérant,
racines, et en réitérant,
 admet
admet 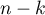 racines, et enfin
racines, et enfin 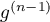 admet 1 racine.
admet 1 racine.
Ainsi, si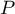 est un polynôme de degré
est un polynôme de degré 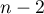 , alors
, alors 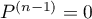 et donc
et donc 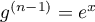 devrait admettre 1 racine, ce qui est absurde.
devrait admettre 1 racine, ce qui est absurde.
Ainsi,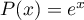 ne peut pas admettre plus de
ne peut pas admettre plus de  racines où
racines où
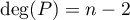 .
.
Ainsi, si
Ainsi,