🔍

Colles de mathématiques

Encadrements sommes et intégrales

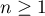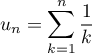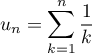On pose, pour $n\geq 1$ , $u_n=\dsp\sum_{k=1}^n\dfrac1k$ et $v_n=u_n-\ln n$ .

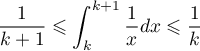Démontrer que, pour tout entier naturel non nul, on a $\dfrac{1}{k+1}\leqslant\dsp\int_k^{k+1}\frac 1xdx\leqslant \dfrac1k$ .
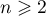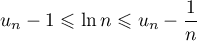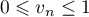En déduire que pour tout entier $n\geqslant2$ , on a $u_n-1\leqslant\ln n\leqslant u_n-\dfrac 1n$ et $0\leqslant v_n\leq 1$ .
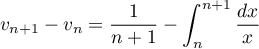Démontrer que pour tout entier naturel non nul, $v_{n+1}-v_n=\dfrac1{n+1}-\int_n^{n+1}\dfrac{dx}x$ .
En déduire que la suite 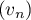converge vers une limite 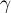$\gamma$ (que l'on ne cherchera pas à calculer).
Que dire de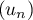 ?