🔍

Colles de mathématiques

Encadrements sommes et intégrales


Sujet


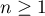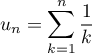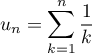On pose, pour n\geq 1, u_n=\dsp\sum_{k=1}^n\dfrac1k  et  v_n=u_n-\ln n.
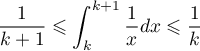  1. Démontrer que, pour tout entier naturel k non nul, on a   \dfrac{1}{k+1}\leqslant\dsp\int_k^{k+1}\frac 1xdx\leqslant \dfrac1k.
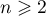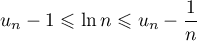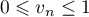  2. En déduire que pour tout entier n\geqslant2, on a u_n-1\leqslant\ln n\leqslant u_n-\dfrac 1n  et  0\leqslant v_n\leq 1.
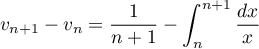  3. Démontrer que pour tout entier naturel non nul,   v_{n+1}-v_n=\dfrac1{n+1}-\int_n^{n+1}\dfrac{dx}x.
  4. En déduire que la suite 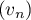(v_n) converge vers une limite 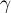\gamma (que l'on ne cherchera pas à calculer).
    Que dire de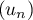 (u_n)?

Corrigé de l'exercice de maths: Intégrales sur un segment

Correction


  1. La fonction 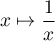$x\mapsto\dfrac1x$ est décroissante sur l'intervalle $[k,k+1]$ et donc on a, pour tout $x\in [k,k+1]$,
    \[\dfrac1{k+1}\leqslant\dfrac1x\leqslant\frac1k\]

    En intégrant ces inégalités, on obtient
    \[\dfrac1{k+1}=\int_k^{k+1}\dfrac1{k+1}dt \leqslant\int_k^{k+1}\dfrac1xdx \leqslant\int_k^{k+1}\frac 1k dt=\dfrac1k\]

  2. En sommant les inégalités précédentes pour $k$ allant de $1$ à $n-1$, le membre de droite de l'inégalité est
    \[1+\frac 12+\dots+\dfrac1{n-1}=u_n-\dfrac1n\]

    Le membre au milieu est alors
    \[\int_1^2\frac 1xdx+\int_2^3\frac 1xdx+\dots+\int_{n-1}^n \frac 1xdx =\int_1^n \frac 1x dx=\ln n\]

    Enfin, le membre de gauche est
    \[\frac 12+\frac13+\dots+\frac 1n=u_n-1\]

    On a ainsi obtenu la première inégalité demandée.

    De plus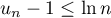 $u_n-1\leq \ln n$ donc $v_n=u_n-\ln n\leq 1$.
    L'autre inégalité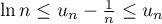 $\ln n\leq u_n-\frac 1n\leq u_n$ donne $v_n=u_n-\ln n\geq 0$.
  3. On a
    \[v_{n+1}-v_n=\dfrac1{n+1}-(\ln (n+1)-\ln n) =\frac 1{n+1}-\int_n^{n+1}\frac{dx}x\]

  4. D'après la question a) et la précédente, on a donc obtenu que 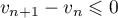$v_{n+1}-v_n\leqslant0$ et donc que la suite 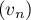$(v_n)$ est décroissante.
    Comme elle est de plus minorée par 0, on en déduit qu'elle est convergente.
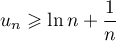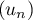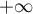    Par ailleurs, de $u_n\geqslant\ln n+\dfrac 1n$ on déduit que $(u_n)$ tend vers $+\infty$.