Colles de mathématiques
Endomorphisme dérivation
Oral ENSAE, Saclay, filière B/L, 2019
Exercice de maths: Annales ENSAE - Saclay - B/L
Sujet
Soit
![\[E=\left\{ x\mapsto (a+bx)e^{2x}+(c+dx)e^{-2x}\,;\ \text{avec } a, b, c, d \in\R\right\}\]](/Generateur-Devoirs/Colles/Applin/endoder/1.png)
- Montrer que
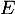est un 
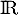-espace vectoriel de dimension finie et en donner une base 
.
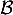- Soit
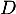une application qui associe à toute fonction de 
sa dérivée.
Montrer que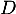
est un endomorphisme de 
.
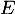Écrire la matrice
de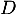 
dans la base 
.
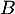Montrer que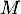
est inversible et calculer son inverse.
- Montrer que toute fonction
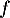de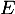 
admet une primitive dans 
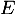, et en donner une expression.