Colles de mathématiques
Endomorphisme dérivation
Oral ENSAE, Saclay, filière B/L, 2019
Sujet
Soit
![\[E=\left\{ x\mapsto (a+bx)e^{2x}+(c+dx)e^{-2x}\,;\ \text{avec } a, b, c, d \in\R\right\}\]](/Generateur-Devoirs/Colles/Applin/endoder/1.png)
- Montrer que
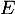 est un
est un 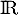 -espace vectoriel de dimension finie et en donner une base
-espace vectoriel de dimension finie et en donner une base 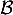 .
.
- Soit
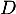 une application qui associe à toute fonction de
une application qui associe à toute fonction de  sa dérivée.
sa dérivée.
Montrer que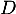 est un endomorphisme de
est un endomorphisme de 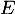 .
.
Écrire la matrice de
de 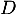 dans la base
dans la base 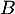 .
.
Montrer que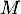 est inversible et calculer son inverse.
est inversible et calculer son inverse.
- Montrer que toute fonction
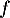 de
de 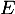 admet une primitive dans
admet une primitive dans 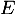 , et en donner une expression.
, et en donner une expression.
Corrigé de l'exercice de maths: Annales ENSAE - Saclay - B/L
Correction
Oral ENSAE - Saclay - 2019
- Soit
 ,
,
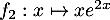 ,
,
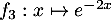 ,
et
,
et
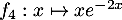 ,
alors
,
alors
 et donc
et donc
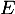 est un sous-espace vectoriel de
est un sous-espace vectoriel de 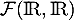 ,
,
Il reste à montrer que la famille de ces quatre fonctions est libre, donc une base.
Soit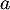 ,
,  ,
,  et
et  quatre réels tels que
quatre réels tels que
![\[af_1+bf_2+cf_3+df_4=0\]](/Generateur-Devoirs/Colles/Applin/endoder_c/12.png)
c'est-à-dire,
![\[\forall x\in\R, \
ae^{2x}+bxe^{2x}+ce^{-2x}+dxe^{-2x}=0\]](/Generateur-Devoirs/Colles/Applin/endoder_c/13.png)
En prenant par exemple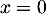 , on obtient
, on obtient 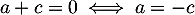 .
.
En factorisant par pour
pour 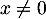 , on a
, on a
![\[\dfrac{a}x+b+\dfrac{c}xe^{-4x}+de^{-4x}=0\]](/Generateur-Devoirs/Colles/Applin/endoder_c/18.png)
puis en prenant la limite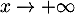 , on obtient
, on obtient 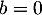 .
.
De même en factorisant par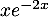 pour
pour  , on a
, on a
![\[\dfrac{a}xe^{4x}+be^{4x}+\dfrac{c}x+d=0\]](/Generateur-Devoirs/Colles/Applin/endoder_c/23.png)
et la limite cette fois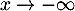 donne alors
donne alors 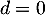 .
On a donc maintenant
.
On a donc maintenant
![\[\forall x\in\R, ae^{2x}+ce^{-2x}=ae^{2x}-ae^{-2x}=0
\iff a\left( e^{2x}-e^{-2x}\rp=0\]](/Generateur-Devoirs/Colles/Applin/endoder_c/26.png)
Il suffit de prendre pour obtenir
pour obtenir  donc
donc  .
.
Finalement, on vient de montrer que la famille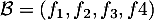 est libre, et comme elle est aussi génératrice, c'est une base de
est libre, et comme elle est aussi génératrice, c'est une base de 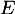 .
.
- On a
![\[D\left( f_1\rp=2f_1\in E\]](/Generateur-Devoirs/Colles/Applin/endoder_c/32.png)
![\[D\left( f_2\rp=f_1+2f_2\in E\]](/Generateur-Devoirs/Colles/Applin/endoder_c/33.png)
![\[D\left( f_3\rp=-2f_3\in E\]](/Generateur-Devoirs/Colles/Applin/endoder_c/34.png)
![\[D\left( f_4\rp=f_3-2f_4\in E\]](/Generateur-Devoirs/Colles/Applin/endoder_c/35.png)
et, comme la dérivation est linéaire, c'est aussi un endomorphisme de
est linéaire, c'est aussi un endomorphisme de 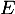 .
.
Dans la base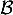 , on a donc la matrice
, on a donc la matrice
![\[M=\lp\begin{array}{cccc}
2&1& 0& 0\\
0&2& 0& 0\\
0&0&-2& 1\\
0&0& 0&-2\enar\rp\]](/Generateur-Devoirs/Colles/Applin/endoder_c/39.png)
Le rang de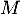 est 4, donc
est 4, donc 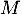 est inversible, avec, après calculs
est inversible, avec, après calculs
![\[M^{-1}=\lp\begin{array}{cccc}
1/2&-1/4& 0& 0\\
0&1/2& 0& 0\\
0&0&-1/2& -1/4\\
0&0& 0&-1/2\enar\rp\]](/Generateur-Devoirs/Colles/Applin/endoder_c/42.png)
- D'après ce qui précède,
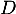 est bijective de
est bijective de 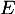 dans
dans  , et en particulier toute fonction
, et en particulier toute fonction 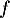 de
de  admet un unique antécédent par
admet un unique antécédent par 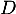 dans
dans 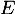 , qui est donc une primitive de
, qui est donc une primitive de 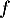 .
.
Soit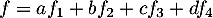 ,
alors la primitive de
,
alors la primitive de 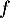 dans
dans  est
est
![\[\begin{array}{ll}D^{-1}(f)&=M^{-1}\lp\begin{array}{c}a\\b\\c\\d\enar\rp\\[2.6em]
&=\lp\begin{array}{c}\dfrac12a-\dfrac14b\\\dfrac12b\\-\dfrac12c-\dfrac14d\\-\dfrac12d\enar\right)
\enar\]](/Generateur-Devoirs/Colles/Applin/endoder_c/54.png)
ou encore, la primitive dans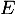 de
de
![\[f:x\mapsto ae^{2x}+bxe^{2x}+ce^{-2x}+dxe^{-2x}\]](/Generateur-Devoirs/Colles/Applin/endoder_c/56.png)
est
![\[F:x\mapsto \lp\dfrac12a-\dfrac14b\right) e^{2x}
+\dfrac12bxe^{2x}
-\lp\dfrac12c+\dfrac14d\right) e^{-2x}
-\dfrac12dxe^{-2x}\]](/Generateur-Devoirs/Colles/Applin/endoder_c/57.png)