Colles de mathématiques
Endomorphismes définis par leurs produits
Oral ENSAE, Saclay, filière B/L, 2014/2015
Retour
Sujet
Soit f et g deux endomorphismes de R2, A et B leurs matrices respectives dans la base canonique.
On suppose que AB = 0 0 0 0 et BA = 0 1 0 0
On suppose que AB = 0 0 0 0 et BA = 0 1 0 0
- f et g peuvent elles être nulles ? Peuvent-elles être bijectives ?
- Déterminer Im(g) et ker(f).
- Donner la forme de A et B.
Corrigé de l'exercice de maths: Applications linéaires - Matrices - Annales ENSAE - Saclay - B/L
Correction
Oral ENSAE - 2014/2015
- Ni f, ni g, ne peut être nulles, car dans ce cas le produit de leurs matrices seraient aussi nul, ce qui n'est pas le cas.
De même, ni f, ni g, ne peut être bijective.
En effet, supposons par exemple f bijective, donc A inversible, alors on aurait
![\[AB=0\iff A^{-1}AB=A^{-1}0=0 \iff B=0\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/14.png)
ce qui donnerait alors aussi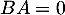 , alors que ce n'est pas le cas.
, alors que ce n'est pas le cas.
- Comme
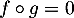 , on a
, on a  .
.
De plus, comme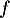 n'est ni nulle ni bijective, on a forcément
n'est ni nulle ni bijective, on a forcément
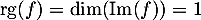 et, par le théorème du rang,
et, par le théorème du rang,
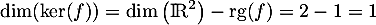 .
.
D'après inclusion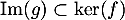 , on a donc aussi nécessairement
, on a donc aussi nécessairement
 .
.
Soit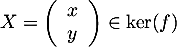 ,
alors
,
alors
![\[AX=0\implies BAX=\lp\begin{array}{c}y\\0\enar\rp=\lp\begin{array}{c}0\\0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/24.png)
d'où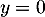 et
et  .
.
- Comme
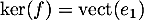 , alors, dans la base canonique
, alors, dans la base canonique
![\[A=\lp\begin{array}{cc}0&a\\0&b\enar\rp\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/28.png)
et de même, comme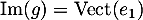 , on a aussi
, on a aussi
![\[B=\lp\begin{array}{cc}c&d\\0&0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/30.png)
ce qui donne
![\[AB=\lp\begin{array}{cc}0&0\\0&0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/31.png)
et
![\[BA=\lp\begin{array}{cc}0&ac+bd\\0&0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/AB-BA_c/32.png)
L'ensemble des matrices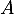 et
et 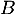 recherchées sont donc celles qui s'écrivent sous la forme précédente, et dont les coefficients vérifient la relation
recherchées sont donc celles qui s'écrivent sous la forme précédente, et dont les coefficients vérifient la relation 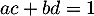 .
.