Colles de mathématiques
Ensemble de matrices stable par produit
Exercice de maths: Matrices
Sujet
Pour 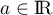 , on pose
, on pose
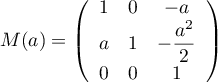 et
et 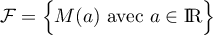 .
.
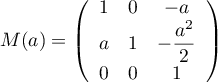 et
et - Montrer que, pour tous réels
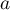 et
et  ,
,
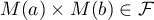 .
.
- Montrer que
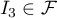
- Montrer que tous les éléments de
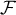 sont inversibles.
sont inversibles.