🔍

Colles de mathématiques

Expression d'une série entière à l'aide d'une équation différentielle


Sujet


On pose f (x) =   ∑ n≥0 x3n/(3n)!.
  1. Déterminer l'ensemble de définition de f.
  2. Calculer f'(x) et f''(x) puis f(x) + f'(x) + f''(x). En déduire f(x).

Corrigé de l'exercice de maths: Séries entières - Équations différentielles

Correction


On pose $f(x)=\dsp\sum_{n\geqslant0}\dfrac{x^{3n}}{(3n)!}$
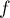  1. $f$ est une série entière et 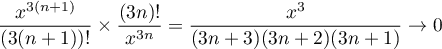$\dfrac{x^{3(n+1)}}{(3(n+1))!}\tm\dfrac{(3n)!}{x^{3n}} =\dfrac{x^3}{(3n+3)(3n+2)(3n+1)}\to0$ pour tout réel $x$.
    Ainsi la série a un rayon de convergence infini, et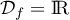 $\mathcal{D}_f=\R$.
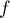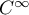  2. En particulier, $f$ est $C^{\infty}$ sur $\R$, et on peut dériver la série terme à terme, d'où
    \[f'(x)=\sum_{n\geqslant1}\dfrac{x^{3n-1}}{(3n-1)!}\]

    et
    \[f"(x)=\sum_{n\geqslant1}\dfrac{x^{3n-2}}{(3n-2)!}\]

    En particulier, on trouve que $f+f'+f"=\dsp\sum_{n\geqslant0}\dfrac{x^n}{n!}=e^x$.

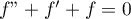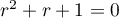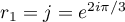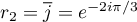    On résout alors cette équation différentielle. L'équation homogène est $f"+f'+f=0$, d'équation caractéristique $r^2+r+1=0$ de racines $r_1=j=e^{2i\pi/3}$ et $r_2=\overline{j}=e^{-2i\pi/3}$ et donc, $y(x)=A\cos\lp\dfrac{2\pi}{3}x\rp+B\sin\lp\dfrac{2\pi}{3}x\rp$. Une solution particulière est $y=\dfrac13x$, d'où la solution générale:
    \[y(x)=A\cos\lp\dfrac{2\pi}{3}x\rp+B\sin\lp\dfrac{2\pi}{3}x\rp +\dfrac13e^x\]


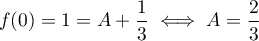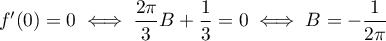    On a de plus $f(0)=1=A+\dfrac13\iff A=\dfrac23$ et $f'(0)=0\iff \dfrac{2\pi}{3}B+\dfrac13=0\iff B=-\dfrac{1}{2\pi}$.
    On trouve donc, finalement, que
    \[f(x)=\dfrac23\cos\lp\dfrac{2\pi}{3}x\right) -\dfrac{1}{2\pi}\sin\lp\dfrac{2\pi}{3}x\right) +\dfrac13e^x\]