Colles de mathématiques
Formule de Taylor-Young avec reste intégral - Énoncé et démonstration
Sujet
Énoncer et démontrer la formule de Taylor-Young avec reste intégral.
Corrigé de l'exercice de math
Correction
Théorème: Soit
f une fonction de classe
Cn+1 sur
[a, b], alors
![\[\begin{array}{ll}
f(b)&\dsp=f(a)+(b-a)f'(a)+\dfrac{(b-a)^2}{2!}f''(a)+\dots+
\dfrac{(b-a)^n}{n!}f^{(n)}(a)+
\int_a^b\dfrac{(b-t)^n}{n!}f^{(n+1)}(t)\,dt \\[1em]
&\dsp=f(a)+\sum_{k=1}^n\dfrac{(b-a)^k}{k!}
+\int_a^b\dfrac{(b-t)^n}{n!}f^{(n+1)}(t)\,dt
\enar\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/4.png)
Démonstration:
On peut démontrer cette formule par récurrence en intégrant par parties le reste intégral:
![\[\int_a^b u'v=\bigl[ uv\bigr]_a^b-\int_a^buv'\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/5.png)
avec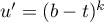 donc
donc  ,
et
,
et 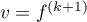 donc
donc 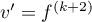 ce qui donne la formule:
ce qui donne la formule:
![\[\begin{array}{ll}
\dsp\int_a^b\dfrac{(b-t)^k}{k!}f^{(k+1)}(t)\,dt
&\dsp=\left[ -\dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+1)}(t) \rb_a^b
-\int_a^b -\dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t) \\[1.4em]
&\dsp=\dfrac{(b-a)^{k+1}}{(k+1)!}
+\int_a^b \dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/10.png)
Ainsi, soit une fonction de classe
une fonction de classe  sur
sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/13.png) .
.
Initialisation: pour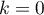 la formule correspond à la définition
de l'intégrale:
la formule correspond à la définition
de l'intégrale:
![\[\int_a^b \dfrac{(b-t)^0}{0!}f^{(1)}(t)\,dt
=\int_a^bf'(t)\,dt=f(b)-f(a)\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/15.png)
soit exactement
![\[f(b)=f(a)+\int_a^b \dfrac{(b-t)^0}{0!}f^{(1)}(t)\,dt\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/16.png)
et la formule est donc vraie.
Hérédité: Supposons maintenant que la formule soit vraie à un rang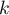 :
:
![\[f(b)=f(a)+\sum_{p=1}^k\dfrac{(b-a)^p}{p!}
+\int_a^b\dfrac{(b-t)^p}{p!}f^{(n+1)}(t)\,dt
\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/18.png)
On a alors, en utilisant la formule obtenue en intégrant par parties:
![\[f(b)=f(a)+\sum_{p=1}^k\dfrac{(b-a)^p}{p!}
+\dfrac{(b-a)^{k+1}}{(k+1)!}
+\int_a^b \dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t) \]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/19.png)
et la formule est encore vrie au rang suivant .
.
Conclusion: D'après le principe de récurrence, la formule de Taylor-Young avec reste intégral est donc vraie pour tout entier , tant que
, tant que 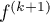 existe sur
existe sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/23.png) ,
en particulier, elle est vraie au rang
,
en particulier, elle est vraie au rang
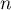 car
car 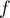 est supposée de classe
est supposée de classe 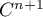 .
.
![\[\begin{array}{ll}
f(b)&\dsp=f(a)+(b-a)f'(a)+\dfrac{(b-a)^2}{2!}f''(a)+\dots+
\dfrac{(b-a)^n}{n!}f^{(n)}(a)+
\int_a^b\dfrac{(b-t)^n}{n!}f^{(n+1)}(t)\,dt \\[1em]
&\dsp=f(a)+\sum_{k=1}^n\dfrac{(b-a)^k}{k!}
+\int_a^b\dfrac{(b-t)^n}{n!}f^{(n+1)}(t)\,dt
\enar\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/4.png)
Démonstration:
On peut démontrer cette formule par récurrence en intégrant par parties le reste intégral:
![\[\int_a^b u'v=\bigl[ uv\bigr]_a^b-\int_a^buv'\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/5.png)
avec
![\[\begin{array}{ll}
\dsp\int_a^b\dfrac{(b-t)^k}{k!}f^{(k+1)}(t)\,dt
&\dsp=\left[ -\dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+1)}(t) \rb_a^b
-\int_a^b -\dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t) \\[1.4em]
&\dsp=\dfrac{(b-a)^{k+1}}{(k+1)!}
+\int_a^b \dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/10.png)
Ainsi, soit
Initialisation: pour
![\[\int_a^b \dfrac{(b-t)^0}{0!}f^{(1)}(t)\,dt
=\int_a^bf'(t)\,dt=f(b)-f(a)\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/15.png)
soit exactement
![\[f(b)=f(a)+\int_a^b \dfrac{(b-t)^0}{0!}f^{(1)}(t)\,dt\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/16.png)
et la formule est donc vraie.
Hérédité: Supposons maintenant que la formule soit vraie à un rang
![\[f(b)=f(a)+\sum_{p=1}^k\dfrac{(b-a)^p}{p!}
+\int_a^b\dfrac{(b-t)^p}{p!}f^{(n+1)}(t)\,dt
\]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/18.png)
On a alors, en utilisant la formule obtenue en intégrant par parties:
![\[f(b)=f(a)+\sum_{p=1}^k\dfrac{(b-a)^p}{p!}
+\dfrac{(b-a)^{k+1}}{(k+1)!}
+\int_a^b \dfrac{(b-t)^{k+1}}{(k+1)!}f^{(k+2)}(t) \]](/Generateur-Devoirs/Colles/Calcul/exTYRI0_c/19.png)
et la formule est encore vrie au rang suivant
Conclusion: D'après le principe de récurrence, la formule de Taylor-Young avec reste intégral est donc vraie pour tout entier