Colles de mathématiques
Limite classique exponentielle
Sujet
Étudier la limite de la suite 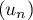 définie
par, pour tout entier non nul
définie
par, pour tout entier non nul 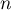 ,
,
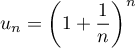
Corrigé de l'exercice de maths: Suites - Limite - Équivalents - Développements limités
Correction
On a 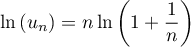 ,
or
,
or  lorsque
lorsque 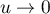 .
.
On a donc, ,
ce qui montre que
,
ce qui montre que
 .
.
On a donc,