Colles de mathématiques
Suite récurrente avec une racine carrée
Exercice de maths: Suites
Sujet
Soit  et
et 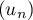 la suite définie par récurrence par
la suite définie par récurrence par 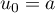 et
et
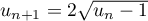 pour
pour 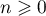 .
.
- Soit
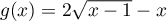 pour
pour 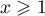 .
Étudier le signe de
.
Étudier le signe de  .
.
- Étudier la convergence de la suite
 .
.
- On pose
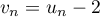 . Montrer que
. Montrer que
![\[\dfrac1{v_{n+1}}-\dfrac1{v_n}\underset{n\to+\infty}{\longrightarrow}\dfrac14\]](/Generateur-Devoirs/Colles/Suites/SR-racine/11.png)