Colles de mathématiques
Matrice d'une application linéaire. Bijective ? Changement de base.
Retour
Sujet
Soit f : R3R3, définie par
f (x, y, z)
= (
x − 2y + z, y − z, 2x − y − z)
- Monter que f est linéaire et donner sa matrice dans la base canonique de R3.
- f est-elle bijective ?
- Donner un vecteur u∈R3 non nul du noyau de f.
- Montrer que (u, e1, f (e1)) est une base de R3.
Donner alors la matrice de f dans cette base.
Corrigé de l'exercice de maths: Applications linéaires - Matrices - Déterminants
Correction
- f est clairement linéaire (à savoir démonter …) et sa matrice dans la base canonique de R3 est:
![\[\lb\begin{array}{rrr}1&-2&1 \\ 0&1&-1 \\ 2&-1&-1\enar\rb\]](/Generateur-Devoirs/Colles/determinants/exApplication-lineaire-bijective-changement-bases_c/4.png)
- On calcule le déterminant de f.
La somme des 3 colonnes donne le vecteur nul;
ce déterminant est donc nul, et f n'est pas bijective.
On peut aussi, alternativement, utiliser la question suivante, à faire donc en même temps: le noyau de f n'est pas réduit au vecteur nul, donc f n'est pas injective, donc pas bijective non plus. - Soit u(x, y, z)∈R3,
alors
![\[u\in\ker(f)
\iff\la\begin{array}{rcl} x-2y+z&=&0 \\ y-z&=&0\\2x-y-z&=&0\enar\right.
\iff x=y=z\]](/Generateur-Devoirs/Colles/determinants/exApplication-lineaire-bijective-changement-bases_c/8.png)
Ainsi, u(1, 1, 1)∈ker(f ). - On a
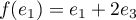 , et donc le déterminant de la famille
, et donc le déterminant de la famille
 s'écrit dans la base canonique,
s'écrit dans la base canonique,
![\[\left|\begin{array}{rrr} 1&1&1 \\ 1&0&0 \\1&0&2 \enar\right|
=-2\not=0\]](/Generateur-Devoirs/Colles/determinants/exApplication-lineaire-bijective-changement-bases_c/12.png)
Cette famille est donc libre, donc aussi une base de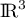 .
.
On a directement, , et
, et 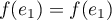 pour les images des
deux premiers vecteurs de cette base, donc dans cette bse la matrice
de
pour les images des
deux premiers vecteurs de cette base, donc dans cette bse la matrice
de 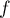 s'écrit:
s'écrit:
 .
.
Il reste à déterminer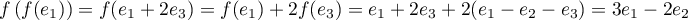 .
.
On cherche donc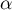 ,
, 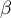 et
et 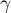 tels que
tels que
![\[f(f(e_1))=\lp\begin{array}{c}3\\-2\\0\enar\rp=\alpha u+\beta e_1+\gamma f(e_1)
=\alpha\lp\begin{array}{c}1\\1\\1\enar\right)
+\beta\lp\begin{array}{c}1\\0\\0\enar\right)
+\gamma\lp\begin{array}{c}1\\0\\2\enar\rp\]](/Generateur-Devoirs/Colles/determinants/exApplication-lineaire-bijective-changement-bases_c/22.png)
On trouve facilement, d'abord (2ème ligne) ,
puis (3ème ligne)
,
puis (3ème ligne)  , et enfin
, et enfin 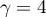 .
Ainsi, dans la base
.
Ainsi, dans la base 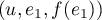 , la matrice de
, la matrice de  est
est
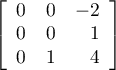 .
.