Colles de mathématiques
Polynôme définissant par une relation avec sa dérivée
Exercice de maths: Polynômes
Sujet
Soit ![$P\in\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5/1.png) un polynôme non nul qui vérifie
un polynôme non nul qui vérifie
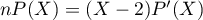 .
.
- Déterminer le degré de
 . En déduire que
. En déduire que 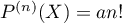 ,
avec
,
avec 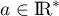 .
.
- Montrer, par récurrence sur
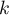 , que, pour tout entier
, que, pour tout entier 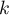 ,
,
![\[P^{(k)}(X)=\dfrac1n\Bigl((X-2)P^{(k+1)}(X)+kP^{(k)}(X)\Bigr)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP5/8.png)
- Montrer que
 pour
pour 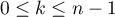 .
.
- En déduire
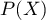 en fonction de
en fonction de 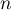 et
et 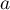 .
.