🔍

Colles de mathématiques

Probabilité d'au moins un événement

Oral ENSAE, Saclay, filière B/L, 2017


Sujet


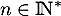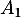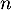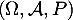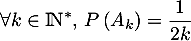Soit $n\in\N^*$ et $A_1$, … $A_n$, $n$ événements indépendants d'un espace probabilisé $\lp\Omega,\mathcal{A},P\rp$ tels que: $\forall k\in\N^*, \, P\left( A_k\rp=\dfrac1{2k}$.
Soit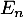 $E_n$ l'événément "Au moins un des 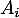$A_i$ est réalisé".
  1. Calculer $P(E_n)$.
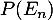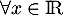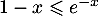  2. Montrer que, $\forall x\in\R$,  $1-x\leqslant e^{-x}$.
    En déduire que: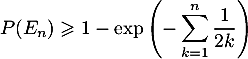 $P(E_n)\geqslant1-\exp\lp-\dsp\sum_{k=1}^n\dfrac1{2k}\rp$.
  3. Calculer 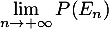$\dsp\lim_{n\to+\infty}P(E_n)$. Interpréter ce résultat.

Corrigé de l'exercice de maths: Probabilités conditionnelles - indépendance - Annales ENSAE - Saclay - B/L

Correction


Corrigé - Oral ENSAE - 2017
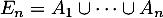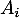  1. On a $E_n=A_1\cup \dots\cup A_n$ et donc, en utilisant le contraire, comme les événements $A_i$ sont indépendants,
    \[\begin{array}{ll}P(E_n)&=P\left( A_1\cup \dots\cup A_n\rp\\[.5em] &=1-P\lp\overline{A_1\cup \dots\cup A_n}\rp\\[.5em] &=1-P\lp\overline{A_1}\cap\dots\cap\overline{A_n}\rp\\ &=1-\dsp\prod_{k=1}^nP\lp\overline{A_k}\rp\\ &=1-\dsp\prod_{k=1}^n\lp1-\dfrac1{2k}\right) \enar\]

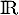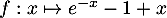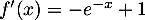  2. On définit sur $\R$ la fonction $f:x\mapsto e^{-x}-1+x$, qui est dérivable avec $f'(x)=-e^{-x}+1$.
    On a alors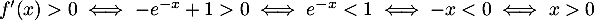 $f'(x)>0\iff -e^{-x}+1>0\iff e^{-x}<1\iff -x <0\iff x>0$, et donc
    \[\begin{tabular}{|c|ccccc|}\hline $x$ &$-\infty$ &&0&&$+\infty$ \\\hline $f'(x)$ &&$-$ &\zb& $+$ &\\\hline &&&&&\\ $f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\ &&&0&&\\\hline \end{tabular}\]

    ce qui montre en particulier que, pour tout réel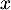 $x$, on a $f(x)\geqslant0$ qui est l'inégalité recherchée.

    On applique alors cette inégalité avec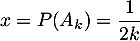 $x=P(A_k)=\dfrac1{2k}$, soit
    \[1-\dfrac1{2k}\leqslant e^{-\frac1{2k}}\]

    et donc, par produit de termes positifs,
    \[\prod_{k=1}^n\lp1-\dfrac1{2k}\rp\leqslant\prod_{k=1}^ne^{-\frac1{2k}} =\exp\lp-\sum_{k=1}^n\dfrac1{2k}\rp\]

    et alors,
    \[P(E_n)=1-\dsp\prod_{k=1}^n\lp1-\dfrac1{2k}\right) \geqslant1-\exp\lp-\sum_{k=1}^n\dfrac1{2k}\rp\]

  3. Pour une probabilité, on a nécessairement 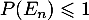$P(E_n)\leqslant1$ et donc
    \[1-\exp\lp-\sum_{k=1}^n\dfrac1{2k}\rp\leqslant P(E_n)\leqslant1\]

    Or, la série harmonique
    \[\sum \dfrac1k\]

    est divergente (ou aussi car c'est une série de Riemann divergente), c'est-à-dire ici, pour une série à termes positifs,
    \[\lim_{n\to+\infty}\sum_{k=1}^n\dfrac1k=+\infty\]

    et donc
    \[\lim_{n\to+\infty}\exp\lp-\sum_{k=1}^n\dfrac1k\rp=0\]

    et enfin, par le théorème des gendarmes, on obtient
    \[\lim_{n\to+\infty}P(E_n)=1\]

    Ce résultat signifie quand prenant un grand nombre d'événements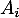 $A_i$ aléatoires indépendants, un au moins finit par se réaliser.