Colles de mathématiques
Probabilité d'au moins un événement
Oral ENSAE, Saclay, filière B/L, 2017
Exercice de maths: Probabilités conditionnelles - indépendance - Annales ENSAE - Saclay - B/L
Sujet
Soit 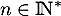 et
et 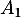 , …
, …  ,
, 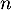 événements indépendants d'un espace probabilisé
événements indépendants d'un espace probabilisé 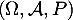 tels que:
tels que:
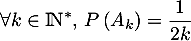 .
.
Soit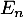 l'événément "Au moins un des
l'événément "Au moins un des 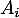 est réalisé".
est réalisé".
Soit
- Calculer
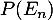 .
.
- Montrer que,
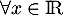 ,
, 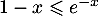 .
.
En déduire que: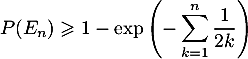 .
.
- Calculer
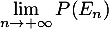 . Interpréter ce résultat.
. Interpréter ce résultat.