Colles de mathématiques
Série entière presque géométrique
Retour
Sujet
Donner le rayon de convergence et donner une expression à l'aide de fonctions usuelles de la série
∑
n≥0
x3n3n + 1.
Corrigé de l'exercice de maths: Séries entières - Intégrales sur un segment
Correction
Si  est le terme général de la série,
on a
est le terme général de la série,
on a 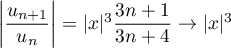 lorsque
lorsque 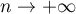 .
.
Le rayon de convergence de cette série entière est donc 1, et on suppose donc dans les tous les calculs à venir que .
.
Soit donc, pour ,
, 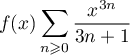 .
.
On pose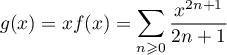 .
.
On a alors, la série entière étant dérivable, et terme à terme, dans son disque de convergence,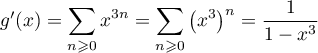 .
.
Il reste maintenant à intégrer.
On décompose en éléments simples
![\[\begin{array}{ll}\dfrac1{1-x^3}
&=\dfrac1{(1-x)(1+x+x^2)}\\[.7em]
&=\dfrac{\alpha}{1-x}+\dfrac{\beta x+\gamma}{1+x+x^2}\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/9.png)
En multipliant par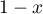 puis en prenant
puis en prenant  on trouve
on trouve  .
.
En multipliant par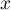 et en faisant tendre
et en faisant tendre 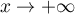 , on obtient
, on obtient  ,
soit
,
soit 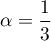 .
.
Enfin, en prenant , on obtient
, on obtient 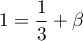 soit
soit 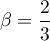 .
.
On a donc
![\[g'(x)=\dfrac13\lb\dfrac1{1-x}+\dfrac{x+2}{1+x+x^2}\rb\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/20.png)
Le premier terme s'intègre directement en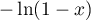 .
.
On décompose encore le second terme:
![\[\dfrac{x+2}{1+x+x^2}
=\dfrac12\tm\dfrac{2x+1}{1+x+x^2}+\dfrac32\tm\dfrac1{1+x+x^2}\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/22.png)
Là aussi le premier terme s'intègre directement en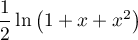 , pour le second on écrit (classiquement)
, pour le second on écrit (classiquement)
![\[\begin{array}{ll}h(x)&=\dsp\int\dfrac{dx}{1+x+x^2}\\[1em]
&=\dsp\int\dfrac{dx}{\left( x+\dfrac12\rp^2+\dfrac34}\\[2.2em]
&=\dsp\int\dfrac{dx}{\dfrac34\left( \dfrac43\left( x+\dfrac12\rp^2+1\rp}\\[2.6em]
&=\dfrac43\dsp\int\dfrac{dx}{\lp\dfrac{2x+1}{\sqrt3}\rp^2+1}
\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/24.png)
Avec le changement de variable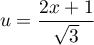 ,
donc
,
donc 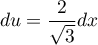 , on a
, on a
![\[\begin{array}{ll}h(x)&=\dfrac43\dsp\int\dfrac{\frac{\sqrt3}{2}du}{u^2+1} \\[1.2em]
&=\dfrac{2\sqrt3}{3}\arctan(u)\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/27.png)
On a donc finalement obtenu
![\[g(x)=\dfrac13\lb-\ln(1-x)+\dfrac12\ln\lp1+x+x^2\right)
+\sqrt3\arctan\lp\dfrac{2x+1}{\sqrt3}\rp\rb+C\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/28.png)
où est une constante d'intégration: comme
est une constante d'intégration: comme 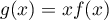 , on a
, on a
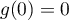 ,
or
,
or
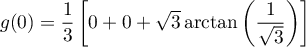 et donc
et donc 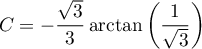 .
.
On a donc obtenu finalement,
![\[\begin{array}{lcl}f(x)&=&\dfrac{g(x)}{x} \\[1.2em]
&=&-\dfrac1{3x}\ln(1-x)+\dfrac1{6x}\ln\lp1+x+x^2\rp\\[.8em]
&&+\dfrac{\sqrt3}{3}\lp\arctan\lp\dfrac{2x+1}{\sqrt3}\rp-\arctan\lp\dfrac1{\sqrt3}\rp\rp
\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/34.png)
Le rayon de convergence de cette série entière est donc 1, et on suppose donc dans les tous les calculs à venir que
Soit donc, pour
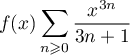 .
.
On pose
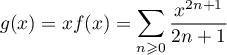 .
.
On a alors, la série entière étant dérivable, et terme à terme, dans son disque de convergence,
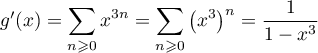 .
.
Il reste maintenant à intégrer.
On décompose en éléments simples
![\[\begin{array}{ll}\dfrac1{1-x^3}
&=\dfrac1{(1-x)(1+x+x^2)}\\[.7em]
&=\dfrac{\alpha}{1-x}+\dfrac{\beta x+\gamma}{1+x+x^2}\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/9.png)
En multipliant par
En multipliant par
Enfin, en prenant
On a donc
Le premier terme s'intègre directement en
On décompose encore le second terme:
Là aussi le premier terme s'intègre directement en
![\[\begin{array}{ll}h(x)&=\dsp\int\dfrac{dx}{1+x+x^2}\\[1em]
&=\dsp\int\dfrac{dx}{\left( x+\dfrac12\rp^2+\dfrac34}\\[2.2em]
&=\dsp\int\dfrac{dx}{\dfrac34\left( \dfrac43\left( x+\dfrac12\rp^2+1\rp}\\[2.6em]
&=\dfrac43\dsp\int\dfrac{dx}{\lp\dfrac{2x+1}{\sqrt3}\rp^2+1}
\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/24.png)
Avec le changement de variable
![\[\begin{array}{ll}h(x)&=\dfrac43\dsp\int\dfrac{\frac{\sqrt3}{2}du}{u^2+1} \\[1.2em]
&=\dfrac{2\sqrt3}{3}\arctan(u)\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/27.png)
On a donc finalement obtenu
où
On a donc obtenu finalement,
![\[\begin{array}{lcl}f(x)&=&\dfrac{g(x)}{x} \\[1.2em]
&=&-\dfrac1{3x}\ln(1-x)+\dfrac1{6x}\ln\lp1+x+x^2\rp\\[.8em]
&&+\dfrac{\sqrt3}{3}\lp\arctan\lp\dfrac{2x+1}{\sqrt3}\rp-\arctan\lp\dfrac1{\sqrt3}\rp\rp
\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exSEPG3_c/34.png)