Colles de mathématiques
Somme des entiers impairs
Sujet
Montrer par récurrence que
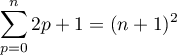 .
.
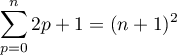 .
.
Corrigé de l'exercice de maths: Sommes - Récurrence
Correction
Par récurrence sur 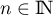 :
:
Pour ,
,
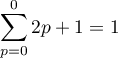 et
et 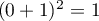 , ce qui montre que la formule est vraie initialement au rang
, ce qui montre que la formule est vraie initialement au rang  .
.
Supposons maintenant que la formule est vraie à un rang quelconque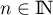 ,
c'est-à-dire
que
,
c'est-à-dire
que 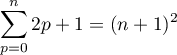 .
.
On a alors, au rang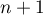 suivant:
suivant:
![\[\begin{array}{ll}\dsp\sum_{p=0}^{n+1} 2p+1
&=\dsp\sum_{p=0}^n 2p+1+(2(n+1)+1)\\[.6em]
&=(n+1)^2+(2n+3) \\[.6em]
&=n^2+4n+4 \\[.5em]
&=(n+2)^2 \\[.5em]
=\bigl((n+1)+1\bigr)^2
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiersImpairs_c/9.png)
et la formule est donc encore vraie.
On a donc montré, grâce au principe de récurrence, que pour tout entier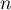 ,
,
 .
.
Pour
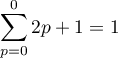 et
et Supposons maintenant que la formule est vraie à un rang quelconque
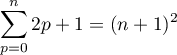 .
.
On a alors, au rang
![\[\begin{array}{ll}\dsp\sum_{p=0}^{n+1} 2p+1
&=\dsp\sum_{p=0}^n 2p+1+(2(n+1)+1)\\[.6em]
&=(n+1)^2+(2n+3) \\[.6em]
&=n^2+4n+4 \\[.5em]
&=(n+2)^2 \\[.5em]
=\bigl((n+1)+1\bigr)^2
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiersImpairs_c/9.png)
et la formule est donc encore vraie.
On a donc montré, grâce au principe de récurrence, que pour tout entier
 .
.