🔍

Colles de mathématiques

Système d'équations aux dérivées partielles


Sujet


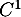Déterminer toutes les fonctions $f:\R^2\to\R$ de classe $C^1$ solutions des systèmes suivants :
\[\left\{ \begin{array}{rcl} \dfrac{\partial f}{\partial x}&=&e^xy\\[3mm] \dfrac{\partial f}{\partial y}&=&e^x+2y. \end{array}\right.\]


Corrigé de l'exercice de maths: Fonctions de plusieurs variables

Correction


La première relation nous donne
\[f(x,y)=ye^x+g(y)\]

où la fonction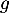 $g$ est quelconque (mais dérivable et d'une seule variable, ainsi 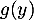$g(y)$ est une constante pour la variable $x$). Cette expression nous donne alors, dans la seconde relation,
\[\dfrac{\partial f}{\partial y}(x,y)=e^x+g'(y)=e^x+2y\]

ce qui nous donne donc
\[g'(y)=2y\iff g(y)=y^2+k\]

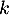où $k$ est un nombre réel quelconque. Ainsi, on a trouvé que si uen fonction vérifie le système donné, alors
\[f(x,y)=ye^x+y^2+k\]

Réciproquement, on vérifie bien que ces fonctions conviennent, et donc qu'on a bien là toutes les solutions.