🔍

Colles de mathématiques

Trace de matrices symétriques

Oral ENSAE, Saclay, filière B/L, 2019


Sujet


Pour quelles matrices A de ℳm,n(R) a-t-on: Tr(AT A) = 0 ?

Corrigé de l'exercice de maths: Matrices - Annales ENSAE - Saclay - B/L

Correction


Oral ENSAE - Saclay

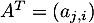Si $A=\left( a_{i,j}\rp$, alors $A^T=\left( a_{j,i}\rp$ et $B=A^T\,A$ a les coefficients
\[b_{i,j}=\sum_{k=1}^m a_{i,k}a_{j,k}\]

et donc
\[Tr(A^T\, A)=Tr(B)=\sum_{i=1}^m b_{i,i} =\sum_{i=1}^m \sum_{k=1}^m a_{i,k}a_{i,k} =\sum_{i=1}^m \sum_{k=1}^m a_{i,k}^2\]

Cette somme de carré est nulle si et seulement si tous les termes sont nuls, et donc, il n'y a qu'une seule matrice correspondante: la matrice nulle.