Théorème de Rolle et accroissements finis

Démonstration:
Géométriquement, ce théorème signifie que la courbe de f admet (au moins) une tangente horizontale:
La démonstration peut être vue comme une conséquence de la propriété des fonctions continues: si f est continue sur [a; b], alors f est bornée et atteint ses bornes.
f atteint par exemple en c un maximum ou un minimum et donc f atteint par exemple en c est un point critique c'est-à-dire f '(c) = 0.
Le seul point qui reste à vérifie est que c∈]a; b[, c'est-à-dire que c≠a et c≠b. Ceci est en effet le cas lorsque f n'est pas constante.

Plus précisément, si f est constante sur [a; b], alors pour tout x∈[a; b], on a f '(x) = 0, et le théorème est clairement vérifié.

Sinon, comme f est continue sur [a; b], f y est bornée, et on pose m = inf{f(x) ; x∈[a, b]} et M = sup{f(x) ; x∈[a, b]}.
Comme f n'est pas constante, on a m < M, et soit donc m < f(a) = f(b) soit f(a) = f(b) < M.
Dans le premier cas par exemple, il existe donc c∈]a; b[ tel que f(c) = m et en ce point critique f '(c) = 0.
Le raisonnement est analogue dans le deuxième cas.

On considère un polynôme de degré n qui admet donc n racines réelles. Si toutes les racines α_i de P sont simples et distinctes: α < α₂ < … < α_n alors, en appliquant le théorème de Rolle n −1 fois à la fonction polynôme x ↦P(x) dérivable sur R donc sur chaque intervalle [α_i; α_i+1], on obtient n −1 racines réelles distinctes, car elles appartiennent toutes à des intervalles disjoints ]α_i; α_i+1[, pour P'.

Supposons au contraire que P possède au moins quatre racines réelles distinctes: x₁, x₂, x₃ et x₄.
Le théorème de Rolle appliqué à P sur les intervalles [x₁; x₂], [x₂; x₃] et [x₃; x₄], montre que P' admet alors au moins trois racines x₁', x₂' et x₃', respectivement dans les intervalles ]x₁; x₂[, ]x₂; x₃[ et ]x₃; x₄[.
Ces intervalles sont disjoints et ces trois racines sont donc distinctes.
On réitère alors le théorème de Rolle sur les deux intervalles ]x₁'; x₂'[ et ]x₂'; x₃'[ pour obtenir deux racines x₁'' et x₂'' distinctes du polynôme dérivé seconde P''.
Or, P''(x) = n(n−1)xⁿ⁻² n'admet pas deux racines distinctes.
Le polynôme P doit donc avoir au plus trois racines réelles distinctes.

Démonstration:
Cette dernière égalité se réécrit f '(c) = f (b) − f (a) / b − a ce qui signifie géométriquement la courbe de f admet (au moins) une tangente parallèle à la droite passant par les points de la courbe aux extrémités de l'intervalle:

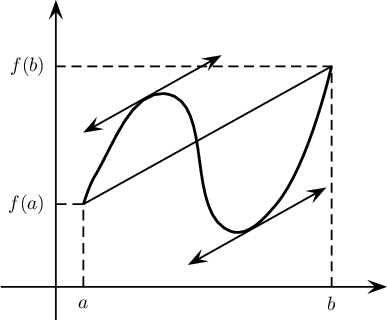
Le coefficient directeur de la sécante passant par (a, f (a)) et (b, f (b)) est m = f (b) − f (a) / b − a
On définit alors la fonction pour laquelle on a φ(a) = φ(b) = 0.
Comme φ est, de même que f, continue sur [a; b] et dérivable sur ]a; b[, on en déduit, d'après le théorème de Rolle, qu'il existe c∈]a; b[ tel que φ'(c) = 0 ⇔ f '(c) − m = 0 soit exactement

Soit f : x ↦ exp(x) définie et dérivable sur R, avec f '(x) = f (x) = exp(x)
Pour tout x réel, d'après le théorème des accroissements finis sur I = ]0; x[ ou I = ]x; 0[, suivant le signe de x, il existe c∈I tel que soit
Ainsi, pour tout x≠0, et alors or c∈]0; x[ ou c∈]x; 0[ et donc |c|≤|x|, et donc d'où et la limite demandée.