Colles de mathématiques
Application linéaire ? Noyau et image ?
Sujet
L'application f : R2R3 définie par f (x, y) = (x + y, x − 2y, 0) est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Corrigé de l'exercice de maths: Applications linéaires
Correction
Soit  et
et 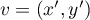 dans
dans 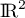 ,
et
,
et 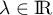 .
Alors :
.
Alors :
![\[\begin{array}{lcl}
f(u+v)&=&\big( (x+x')+(y+y'),(x+x')-2(y+y'),0)\\[.4em]
&=&\big(x+y,x-2y,0)+(x'+y',x'-2y',0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/5.png)
De même,
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+\lambda y,\lambda x+2\lambda y,0)\\[.4em]
&=&\lambda(x+y,x+2y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/6.png)
f est donc une application linéaire.
De plus, soit
![\[\begin{array}{ll}
u(x,y)\in\text{Ker}(u)
&\iff f(u)=0\\[.4em]
&\iff\la\begin{array}{lcl} x+y &=& 0\\ x-2y&=&0 \\0=0 \enar\right. \\
&\iff x=y=0
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/8.png)
Ainsi, Ker(f )={(0,0)}: le noyau de f est réduit au vecteur nul et f est injective.
Le théorème du rang nous fournit que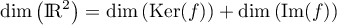 et
donc que
et
donc que 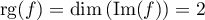 .
.
Plus précisément, Soit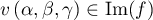 ,
alors il existe
,
alors il existe 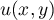 tel que
tel que 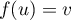 ,
,
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=0\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=0\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/17.png)
Ainsi, tout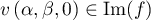 et donc
et donc
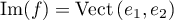 où
où
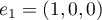 et
et 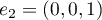 sont les deux premiers vecteurs de la base canonique de
sont les deux premiers vecteurs de la base canonique de 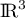 .
.
f n'est donc pas surjective, donc pas non plus bijective (ce qui était clair dès le début car f : R2R3 et dim(R2) = 2≠dim(R3) = 3 ou avec le théorème du rang).
![\[\begin{array}{lcl}
f(u+v)&=&\big( (x+x')+(y+y'),(x+x')-2(y+y'),0)\\[.4em]
&=&\big(x+y,x-2y,0)+(x'+y',x'-2y',0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/5.png)
De même,
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+\lambda y,\lambda x+2\lambda y,0)\\[.4em]
&=&\lambda(x+y,x+2y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/6.png)
f est donc une application linéaire.
De plus, soit
![\[\begin{array}{ll}
u(x,y)\in\text{Ker}(u)
&\iff f(u)=0\\[.4em]
&\iff\la\begin{array}{lcl} x+y &=& 0\\ x-2y&=&0 \\0=0 \enar\right. \\
&\iff x=y=0
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/8.png)
Ainsi, Ker(f )={(0,0)}: le noyau de f est réduit au vecteur nul et f est injective.
Le théorème du rang nous fournit que
Plus précisément, Soit
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=0\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=0\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/17.png)
Ainsi, tout
f n'est donc pas surjective, donc pas non plus bijective (ce qui était clair dès le début car f : R2R3 et dim(R2) = 2≠dim(R3) = 3 ou avec le théorème du rang).