Colles de mathématiques
Bijection et expression de la réciproque
Sujet
Soit
f : [1;+∞[[1;+∞[
définie par
f (x) = exp(ln2x) .
Démontrer que f est une bijection, et déterminer la bijection réciproque
Démontrer que f est une bijection, et déterminer la bijection réciproque
Corrigé de l'exercice de math
Correction
On a
![\[f'(x)=2\tm\dfrac1x\tm\ln x\tm\exp\lp\ln^2 x\rp\]](/Generateur-Devoirs/Colles/Calcul/exFR0_c/1.png)
et donc, pour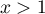 ,on a
,on a 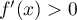 et
et 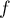 est strictement croissante sur
est strictement croissante sur 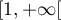 .
.
De plus,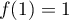 et, par composition de limites,
et, par composition de limites,
![\[\lim_{x\to+\infty}f(x)=+\infty\]](/Generateur-Devoirs/Colles/Calcul/exFR0_c/7.png)
.
En résumé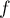 est continue strictement croissante, et réalise donc
une bijection de
est continue strictement croissante, et réalise donc
une bijection de 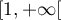 sur
sur 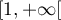 .
.
Soit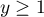 , alors l'équation
, alors l'équation
![\[\begin{array}{ll}f(x)=y&\iff \exp(\ln^2 x)=y\\[.5em]
&\iff \ln^2(x)=\ln(y)\\[.5em]
&\iff \ln(x)=\sqrt{\ln y}\\[.5em]
&\iff x=\exp\left(\sqrt{\ln y}\right)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exFR0_c/12.png)
On a ainsi obtenu l'expression de la fonction réciproque
![\[f^{-1}(y)=\exp\left(\sqrt{\ln y}\right)\]](/Generateur-Devoirs/Colles/Calcul/exFR0_c/13.png)
et donc, pour
De plus,
.
En résumé
Soit
![\[\begin{array}{ll}f(x)=y&\iff \exp(\ln^2 x)=y\\[.5em]
&\iff \ln^2(x)=\ln(y)\\[.5em]
&\iff \ln(x)=\sqrt{\ln y}\\[.5em]
&\iff x=\exp\left(\sqrt{\ln y}\right)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exFR0_c/12.png)
On a ainsi obtenu l'expression de la fonction réciproque