Colles de mathématiques
Décomposition d'un polynôme de degré n
Sujet
Soit 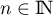 et
et 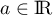 ,
,  ,
, 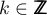 .
.
- Résoudre l'équation
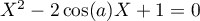
- En déduire une factorisation de
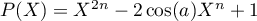 dans
dans ![$\C[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP4/7.png)
- En déduire une factorisation de
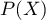 dans
dans ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP4/9.png)
Corrigé de l'exercice de maths: Polynômes - Nombres complexes
Correction
- Le discriminant de ce trinôme du second degré est
![\[\begin{array}{ll}\Delta&=4\cos^2(a)-4=4\lp\cos^2(a)-1\rp\\
&=-4\sin^2(a)\\
&=\lp2i\sin(a)\rp^2\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/1.png)
L'équation admet donc deux racines complexes conjuguées
![\[\alpha=\dfrac{2\cos(a)+2i\sin(a)}{2}=e^{ia}\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/2.png)
et
![\[\overline{\alpha}=e^{-ia}\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/3.png)
- En posant
 , on a
, on a  qui a comme racines
qui a comme racines
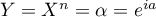 donc
donc 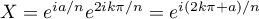 et
et 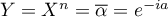 donc
donc
 ,pour tout entier
,pour tout entier 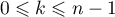 .
.
En notant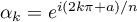 et
et 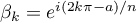 on a donc la factorisation dans
on a donc la factorisation dans ![$\C[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/13.png) :
:
![\[\begin{array}{ll}P(X)&=X^{2n}-2\cos(a)X^n+1\\
&=\dsp\prod_{k=0}^{n-1}\left( X-\alpha_k\rp\left( X-\beta_k\rp
\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/14.png)
- La factorisation de
 dans
dans ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/16.png) s'obtient en effectuant, dans la factorisation précédente,
les produits de polynômes du premier degré dans les racines sont conjuguées:
s'obtient en effectuant, dans la factorisation précédente,
les produits de polynômes du premier degré dans les racines sont conjuguées:
![\[\begin{array}{ll}\overline{\alpha_k}&=e^{-ia/n}e^{-2ik\pi/n}\\
&=e^{-ia/n}e^{-2ik\pi/n+2i\pi}\\
&=e^{-ia}e^{2i\pi(n-k)/n}\\
&=\beta_{n-k}\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/17.png)
et
![\[\begin{array}{ll}\left( X-\alpha_k\rp\left( X-\beta_{n-k}\rp
&=X^2-2\Re e\lp\alpha_k\right) X+\left|\alpha_k\right|^2\\
&=X^2-2\cos\lp\dfrac{2k\pi+a}{n}\right) X+1\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/18.png)
On obtient donc
![\[P(X)=\prod_{k=0}^{n-1}\left( X^2-2\cos\left(\dfrac{2k\pi+a}{n}\right) X+1\right)\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP4_c/19.png)