Colles de mathématiques
Dérivée d'une somme géométrique
Sujet
Pour x∈R
et n∈N*, calculer la somme
n
∑
k=1
kxk−1
Corrigé de l'exercice de maths: Suites - Sommes
Correction
Soit la fonction polynôme 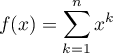 .
.
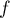 est dérivable sur
est dérivable sur  (et même
(et même 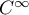 ),
et on a, pour tout réel
),
et on a, pour tout réel 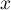 ,
,
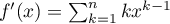 .
.
Par ailleurs, on a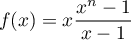 , et donc
, et donc
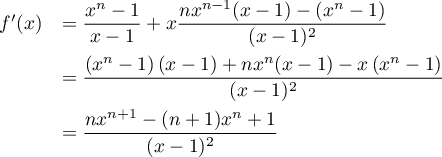
On a ainsi, .
.
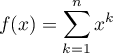 .
.
Par ailleurs, on a
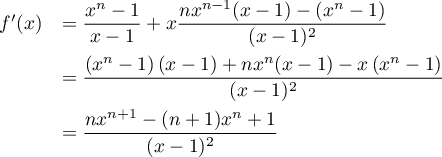
On a ainsi,
 .
.