Colles de mathématiques
Déterminer les polynômes tels que … (quater)
Sujet
On cherche à déterminer les polynômes de ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33/1.png) qu vérifient la relation
qu vérifient la relation
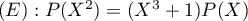 .
.
- Démontrer que le polynôme nul ainsi que le polynôme
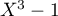 sont
solutions du problème.
sont
solutions du problème.
- Soit
 un polynôme qui vérifie la relation
un polynôme qui vérifie la relation 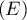 .
.
- Déterminer le degré de
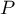 .
.
- Démontrer que
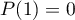 , puis que
, puis que  .
.
- En effectuant la division euclidienne de
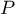 par
par 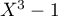 , démontrer
qu'il existe
, démontrer
qu'il existe 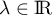 tel que
tel que  .
.
- Déterminer le degré de
- Conclure: quels sont les polynômes de
![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33/1.png) solutions de
solutions de 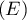 ?
?
Corrigé de l'exercice de maths: Polynômes
Correction
- Le polynôme nul vérifie simplement la relation et,
pour
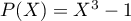 , on a
, on a 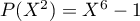 , puis
, puis
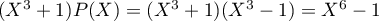 . Ce polynôme est aussi solution.
. Ce polynôme est aussi solution.
-
- Soit
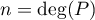 , lors
, lors 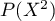 est de degré
est de degré 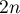 et
et 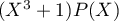 est de degré
est de degré 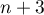 . On doit donc avoir
. On doit donc avoir 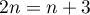 , soit
, soit  .
.
- En évaluant la relation en
 , on a
, on a 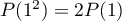 d'où
d'où 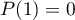 .
.
Pour faire intervenir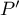 et
et 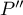 , on dérive maintenant l'équation
, on dérive maintenant l'équation 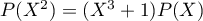 .
On trouve
.
On trouve
![\[2XP'(X^2)=3X^2P(X)+(X^3+1)P'(X)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/17.png)
et, en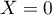 , on trouve
, on trouve 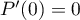 .
.
On dérive alors une second fois. On trouve cette fois
![\[2P'(X^2)+4X^2P''(X^2)=6XP(X)+6X^2P'(X)+(X^3+1)P''(X)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/20.png)
et, en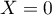 , comme
, comme 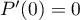 , on trouve maintenant que
, on trouve maintenant que 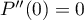 .
.
- La division euclidienne de
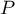 par
par 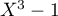 s'écrit
s'écrit
![\[P(X)=Q(X)(X^3-1)+R(X)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/26.png)
où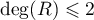 et donc
et donc 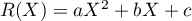 .
.
De plus, comme on a vu que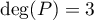 , on a nécessairement
, on a nécessairement 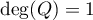 , c'est-à-dire que le polynôme
, c'est-à-dire que le polynôme 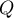 est une constante, soit
est une constante, soit 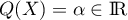 , et donc
, et donc
![\[P(X)=\alpha\left( X^3-1\rp+\left( aX^2+bX+c\rp\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/33.png)
Il reste à montrer que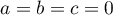 .
.
On a tout d'abord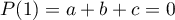 .
.
En dérivant, on obtient
![\[P'(X)=3\lambda X^2+(2aX+b)\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/36.png)
et, puisque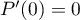 , on a
, on a 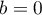 .
.
En dérivant une seconde fois, on obtient
![\[P''(X)=6\lambda X+2a\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/39.png)
et, à nouveau puisque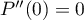 , on a
, on a  et finalement également
et finalement également 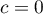 .
.
- Soit
- On a donc montré jusque là que si un polynôme vérifie la relation
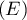 , alors il est soit nul, soit s'écrit sous la forme
, alors il est soit nul, soit s'écrit sous la forme 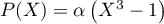 avec
avec 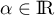 .
.
Il reste à vérifier la réciproque, ce qui est fait dans la première question.
On a donc montré que l'ensemble des solutions de la relation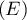 est
est
![\[\Bigl\{\alpha\left( X^3-1\rp;\ \alpha\in\R\Bigr\}\]](/Generateur-Devoirs/Colles/Polynomes/exDeterminerP33_c/47.png)