🔍

Colles de mathématiques

Diagonalisabilité d'une application linéaire entre polynomes

Oral ENS Ulm, filière B/L, 2016


Sujet


  1. Soit A et B deux réels et f : ]0; 1[ R une fonction de classe C1 qui vérifie, pour tout x∈]0; 1[,
    f '(x) = A/x + B/x − 1 f (x)

    Montrer qu'il existe une constante C telle que, pour tout x∈]0; 1[, f (x) = CxA(x − 1)B
    Indication: on pourra considérer la fonction définie par g(x) = f (x)/xA(x − 1)B
  2. Soit un entier n≥2 et l'application Φ: Rn[X] Rn[X] P ↦ X(X−1)P' − n(X+1)P
    1. Montrer que Φ est un endomorphisme de Rn[X].
    2. Soit λ∈R. Montrer qu'il existe deux réels Aλ et Bλ (qui dépendent de λ et n) tels que, pour tout x∈]0; 1[,
      n(x+1) + λ/x(x − 1) = Aλ/x + Bλ/x − 1
    3. Montrer que Φ est diagonalisable.

Corrigé de l'exercice de maths: Diagonalisation - Annales ENS Ulm - B/L

Correction


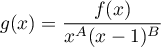  1. Soit $g(x)=\dfrac{f(x)}{x^A(x-1)^B}$. En prenant le logarithme, on a
    \[\ln(g(x))=\ln(f(x))-A\ln(x)-B\ln(x-1)\]

    et alors, en dérivant,
    \[\dfrac{g'(x)}{g(x)}=\dfrac{f'(x)}{f(x)}-\dfrac{A}x-\dfrac{B}{x-1}\]

    et alors,
    \[f'(x)=f(x)\lp\dfrac{A}x+\dfrac{B}{x-1}\rp+\dfrac{g'(x)}{g(x)}\times f(x)\]

    On obtient donc que
    \[f'(x)=f(x)\lp\dfrac{A}x+\dfrac{B}{x-1}\right) \iff \dfrac{g'(x)}{g(x)}\times f(x)=0\]

    et donc, soit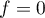 $f=0$, soit 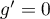$g'=0$ donc $g=c$.
    En revenant à la définition de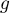 $g$, on a donc 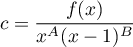$c=\dfrac{f(x)}{x^A(x-1)^B}$, qui est le résultat souhaité sur $f$.
    Remarque: on peut aussi directement dériver la fonction $g$.
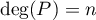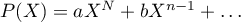    1. Par linéarité de la dérivée, l'application $\phi$ est aussi linéaire. De plus, si $P\in\R_n[X]$, alors $\text{deg}(P)=n$ avec $P(X)=aX^N+bX^{n-1}+\dots$ et alors
      \[\phi(P)=X(X-1)\left( anX^{n-1}+b(n-1)X^{n-2}+\dots\right) -n(X+1)\left( aX^n+bX^{n-1}+\dots\right)\]

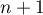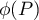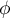      les termes de degré $n+1$ s'annulent, et le polynôme $\phi(P)$ est donc de degré $n$, soit $\phi(P)\in\R_n[X]$, ce qui finit de montrer que $\phi$ est bien un endomorphisme de $\R_n[X]$
    2. Il suffit de mettre sur le même dénominateur:
      \[\dfrac{A_\lambda}x+\dfrac{B_\lambda}{x-1} =\dfrac{\left( A_\lambda+B_\lambda\right) x-A_\lambda}{x(x-1)} =\dfrac{nx+n+\lambda}{x(x-1)}\]

      et on doit donc avoir
      \[\la\begin{array}{ll}A_\lambda+B_\lambda&=n\\-A_\lambda&=n+\lambda\enar\right. \iff\la\begin{array}{ll}A_\lambda&=-n-\lambda\\B_\lambda&=2n+\lambda\enar\right. \]

    3. Soit $\lambda$ une valeur propre de $\phi$, alors il existe un polynôme $P\in\R_n[X]$ non nul tel que
      \[\begin{array}{ll} \phi(P)=\lambda P &\iff X(X-1)P'-n(X+1)P=\lambda P\\[.5em] &\iff P'=\dfrac{n(X+1)+\lambda}{X(X-1)}P\enar\]

      soit, d'après la question précédent,
      \[P'=\lp\dfrac{A_\lambda}X+\dfrac{B_\lambda}{X-1}\right) P\]

      et alors, d'après la première question, il existe une constante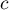 $c$ tel que
      \[P(X)=cX^{A_\lambda}(X-1)^{B_\lambda}\]

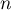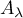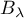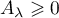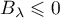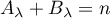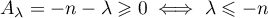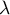      Maintenant, cette expression est un polynôme de degré au plus $n$ lorsque $A_\lambda$ et $B_\lambda$ sont des entiers tels que $A_\lambda\geqslant0$, $B_\lambda\leqslant0$ et $A_\lambda+B_\lambda=n$. D'après la question précédente, la troisième relation est assurée, tandis que les deux autres s'écrivent: $A_\lambda=-n-\lambda\geqslant0\iff \lambda\leqslant-n$ et $B_\lambda=2n+\lambda\geqslant0\iff\lambda\geqslant-2n$. En résumé, $\lambda$ doit être un entier tel que
      \[-2n\leqslant\lambda\leqslant-n\]

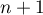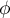      Il y a $n+1$ tels entiers, qui est aussi la dimension de $\R_n[X]$. Ainsi, $\phi$ n' que des valeurs propres simples, et est diagonalisable.