Colles de mathématiques
Endomorphisme dont le carré est l'opposé de l'identité
Sujet
Soit E un espace vectoriel réel de dimension finie, et f un endomorphisme de E vérifiant f 2 = −id.
- Donner un exemple de tel endomorphisme sur R2.
- Montrer que f n'a pas de valeurs propres réelles. En déduire que la dimension de E est paire.
- Montrer que, pour tout x∈E, on a Vect(x, f (x)) est stable par f.
- En déduire que si dim(E) = 2n, il existe des vecteurs e1, … , en, tels que (e1, f(e1), … , f(en), en), forme une base de E. Quelle est la matrice de f dans cette base ?
Corrigé de l'exercice de maths: Diagonalisation
Correction
- Soit f l'endomorphisme dont la matrice dans la base canonique
de R2 est:
![\[\lp\begin{array}{cc}
0&-1\\
1&0\\
\end{array}\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/endo-carre-moins-id_c/3.png)
Un simple calcul matriciel montre que f 2 = −id. - Si
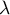 est une valeur propre associée au vecteur propre
est une valeur propre associée au vecteur propre 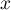 ,
la condition
,
la condition 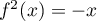 entraîne que
entraîne que 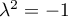 :
il n'existe pas de valeurs propres réelles. Si l'espace était de dimension
impaire, le polynome caractéristique serait de degré impair, et aurait
une racine réelle, ce qui donnerait une valeur propre réelle : impossible!
:
il n'existe pas de valeurs propres réelles. Si l'espace était de dimension
impaire, le polynome caractéristique serait de degré impair, et aurait
une racine réelle, ce qui donnerait une valeur propre réelle : impossible!
- Soit
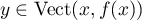 ,
, 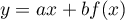 . On a :
. On a :
![\[f(y)=af(x)-bx\in\text{Vect}(x,f(x))\]](/Generateur-Devoirs/Colles/Diagonalisation/endo-carre-moins-id_c/11.png)
- Procédons de proche en proche.
Soit
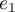 un vecteur non-nul de
un vecteur non-nul de 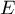 .
. 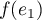 n'est pas lié à
n'est pas lié à  ,
puisque
,
puisque 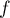 est sans valeur propre.
On choisit ensuite
est sans valeur propre.
On choisit ensuite 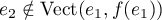 .
Il faut prouver que
.
Il faut prouver que 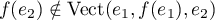 .
Mais si tel était le cas, on aurait
.
Mais si tel était le cas, on aurait
![\[f(e_2)=ae_1+bf(e_1)+ce_2\implies -e_2=af(e_1)-be_1+cf(e_2)\]](/Generateur-Devoirs/Colles/Diagonalisation/endo-carre-moins-id_c/19.png)
et en remplaçant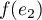 par
par 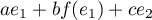 , on trouverait que la
famille
, on trouverait que la
famille 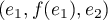 est liée. On continue ainsi pour construire
est liée. On continue ainsi pour construire
 , etc...
La matrice résultante est diagonale par blocs, les
, etc...
La matrice résultante est diagonale par blocs, les 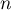 blocs sont ceux apparus à la question 1.
blocs sont ceux apparus à la question 1.