Colles de mathématiques
Endomorphisme de polynômes
Oral HEC - filière B/L, 2022
Exercice de maths: Applications linéaires - Matrices - Diagonalisation - Annales HEC - B/L
Sujet
oral HEC, BL - 2022.
On note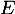 l'espace vectoriel des fonctions polynomiales de degré inférieur ou égal à 2. On définit les fonctions
l'espace vectoriel des fonctions polynomiales de degré inférieur ou égal à 2. On définit les fonctions 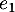 ,
, 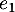 ,
,  par:
par:
![\[e_0(t) = 1 ,\ e_1(t) = t , \ e_2 (t) = t^2\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/5.png)
pour tout réel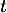 .
.
On rappelle que la famille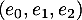 est une base de
est une base de 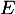 .
On considère l'application
.
On considère l'application  qui, à toute fonction
qui, à toute fonction 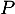 de
de 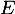 , associe la fonction, notée
, associe la fonction, notée 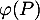 , définie par:
, définie par:
![\[\forall x\in\R,
\varphi(P)(x)=\int_0^1P(x+t)dt\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/13.png)
On note
pour tout réel
On rappelle que la famille
- Question de cours : Critère d'inversibilité d'une matrice triangulaire.
- Montrer que
 est un endomorphisme de
est un endomorphisme de 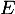 .
.
-
- Écrire la matrice
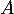 de
de 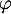 dans la base
dans la base 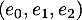 .
.
- Justifier que
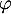 est un automorphisme de
est un automorphisme de 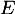 .
.
- L'endomorphisme
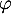 est-il diagonalisable?
est-il diagonalisable?
- Écrire la matrice
-
- Montrer que pour tout entier naturel
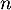 , il existe un réel
, il existe un réel 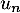 tel que:
tel que:
![\[A^n=\lp\begin{array}{ccc}1&\frac{n}2&u_n\\0&1&n\\0&0&1\enar\rp\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/24.png)
- En déduire, par sommation, l'expression de
 pour tout entier
pour tout entier 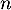 .
.
- Montrer que pour tout entier naturel